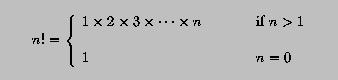
The factorial of a non-negative integer n, written as n!, is defined as follows:
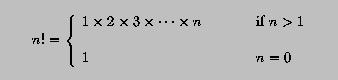
Write a program that reads in an integer and computes its factorial.
This program should detect if the input is negative and display an error
message.
![]()
! ----------------------------------------------------------
! Given a non-negative integer N, this program computes
! the factorial of N. The factorial of N, N!, is defined as
! N! = 1 x 2 x 3 x .... x (N-1) x N
! and 0! = 1.
! ----------------------------------------------------------
PROGRAM Factorial
IMPLICIT NONE
INTEGER :: N, i, Answer
WRITE(*,*) 'This program computes the factorial of'
WRITE(*,*) 'a non-negative integer'
WRITE(*,*)
WRITE(*,*) 'What is N in N! --> '
READ(*,*) N
WRITE(*,*)
IF (N < 0) THEN ! input error if N < 0
WRITE(*,*) 'ERROR: N must be non-negative'
WRITE(*,*) 'Your input N = ', N
ELSE IF (N == 0) THEN ! 0! = 1
WRITE(*,*) '0! = 1'
ELSE ! N > 0 here
Answer = 1 ! initially N! = 1
DO i = 1, N ! for each i = 1, 2, ..., N
Answer = Answer * i ! multiply i to Answer
END DO
WRITE(*,*) N, '! = ', Answer
END IF
END PROGRAM Factorial
Click here to download this program.
This program computes the factorial of a non-negative integer What is N in N! --> -5 ERROR: N must be non-negative Your input N = -5
This program computes the factorial of a non-negative integer What is N in N! --> 0 0! = 1
This program computes the factorial of a non-negative integer What is N in N! --> 5 5! = 120
This program computes the factorial of a non-negative integer What is N in N! --> 13 13! = 1932053504
It is worthwhile to note that most CPU's do not report integer overflow. As a result, on a typical computer today, the maximum factorial is around 13!. If you try this program on a PC, you should get 13! = 1932053504 and 14! = 1278945280. But, 13! > 14! is obviously incorrect. Then, we have 15! = 2004310016, 16! = 2004189184, and 17! = -288522240. These results are obviously wrong. This shows that a typical PC can only handle up to 13!