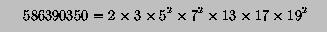
Finding All Prime Factors of a Positive Integer

Problem Statement

As we have learned in high school, any positive integer can be factorized into prime factors. For example, 586390350 can be factorized as follows:

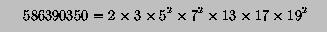
Thus, 586390350 has factors 2, 3, 5, 5,, 7, 7, 13, 17, 19 and 19. Note that all factors are prime numbers.

Write a program that reads in an integer greater than or equal to 2 and finds all of its prime factors.

This problem is a little more difficult than the others and may require longer time to understand its logic.

Solution

! ---------------------------------------------------------------
! This program determines all prime factors of an n integer >= 2.
! It first removes all factors of 2.  Then, removes all factors
! of 3, 5, 7, and so on.  All factors must be prime numbers since
! when a factor is tried all of whose non-prime factors have
! already been removed.
! ---------------------------------------------------------------

PROGRAM  Factorize
   IMPLICIT  NONE

   INTEGER  :: Input
   INTEGER  :: Divisor
   INTEGER  :: Count

   WRITE(*,*)  'This program factorizes any integer >= 2 --> '
   READ(*,*)   Input

   Count = 0
   DO                         ! here, we try to remove all factors of 2
      IF (MOD(Input,2) /= 0 .OR. Input == 1)  EXIT
      Count = Count + 1       ! increase count
      WRITE(*,*)  'Factor # ', Count, ': ', 2
      Input = Input / 2       ! remove this factor from Input
   END DO

   Divisor = 3                ! now we only worry about odd factors
   DO                         ! 3, 5, 7, .... will be tried
      IF (Divisor > Input) EXIT    ! if a factor is too large, exit and done
      DO                      ! try this factor repeatedly
         IF (MOD(Input,Divisor) /= 0 .OR. Input == 1)  EXIT
         Count = Count + 1
         WRITE(*,*)  'Factor # ', Count, ': ', Divisor
         Input = Input / Divisor   ! remove this factor from Input
      END DO
      Divisor = Divisor + 2   ! move to next odd number
   END DO

END PROGRAM  Factorize

Click here to download this program.

Program Input and Output

If the input is 100, the output consists of four factors 2, 2, 5 and 5.

This program factorizes any integer >= 2 -->
100

Factor # 1: 2
Factor # 2: 2
Factor # 3: 5
Factor # 4: 5

If the input is 16, the output consists of four factors 2, 2, 2 and 2.

This program factorizes any integer >= 2 -->
16

Factor # 1: 2
Factor # 2: 2
Factor # 3: 2
Factor # 4: 2

If the input is 53, since it is a prime number, the output has only one factor: 53 itself.
```
This program factorizes any integer >= 2 -->
53

Factor # 1: 53
```

If the input value is 586390350, the output consists of 10 factors 2, 3, 5, 5, 7, 7, 13, 17, 19 and 19.

This program factorizes any integer >= 2 -->
586390350

Factor # 1: 2
Factor # 2: 3
Factor # 3: 5
Factor # 4: 5
Factor # 5: 7
Factor # 6: 7
Factor # 7: 13
Factor # 8: 17
Factor # 9: 19
Factor # 10: 19

Discussion

How to remove a factor from a given number? I believe you have learned it in high school. Let the given number be n and we know x is a factor of n. Then, we just keep dividing n by x until the quotient is 1 or x cannot evenly divide n.
For example, 3 is a factor of 72. The first division yields a quotient 24=72/3. The second division yields a quotient 8=24/3. Thus, the original number 72 has two factors of 3.
If n and x are both 53, then the first division yields a quotient 1=53/53. Since the quotient is 1, no more division is necessary and 53 has a factor 53!
So, how to convert the above idea to a program? Let us use Input and Divisor for n and x, respectively. The following DO-loop will do the job:
```
DO
   IF (MOD(Input,Divisor) /= 0 .OR. Input == 1)  EXIT
   ... since MOD(Input,Divisor)=0 here, Divisor is a factor...
   Input = Input / Divisor
END DO
```
In the above, if Divisor cannot evenly divide Input or Input is 1, we exit the loop. The former condition states that Divisor is not a factor of Input, while the latter means Input is 1 and does not have any other factor.
If both conditions are .FALSE., then Divisor can evenly divide Input and Input is not 1. Therefore, Input is a factor of Divisor. To remove it, just perform a division and this is the meaning of Input = Input / Divisor.
Since 2 is the only even prime number, we'd better remove all factors of 2 before starting any other work. Therefore, letting Divisor to 2 in the above code will remove all factor of 2:
```
DO
   IF (MOD(Input,2) /= 0 .OR. Input == 1)  EXIT
   ... since MOD(Input,2)=0 here, 2 is a factor...
   Input = Input / Divisor
END DO
```
After exiting this loop, we are sure the new value of Input will have no factors of 2. Then, we can try all odd numbers to see some of them could be factors.

To try odd numbers, it is simply the following:

Divisor = 3
DO
   IF (Divisor > Input)  EXIT
   ...remove all factors of Divisor...
   Divisor = Divisor + 2
END DO

Putting everything together, it is the program shown above.
Why the factors found are prime numbers? A good question, indeed.
It is not difficult to answer, however. If Input does have a composite factor (a composite number is the product of several prime numbers), say x = a*b, where a is a prime number. Then, before the program can test if x is a factor, a has been tested since a < x, and the factor a is removed. Consequently, only a possible factor b remains. In other words, composite number x is never tested and the program will not report any composite factors.
Let us factorize 586390350 as an example:
1. Factors of 2 are removed first. Removing the first factor of 2 yields 293195175=586390350/2.
2. Since 293195175 is not even, it has no more factors of 2. So, we shall try all odd numbers: 3, 5, 7, 9, 11, ...
3. Removing a factor of 3 yields 97731725=293195175/3.
4. Since 97731725 has no factors of 3, try 5.
5. Removing a factor of 5 yields 19546345=97731725/5.
6. Removing a factor of 5 a second time yields 3909269=19546345/5.
7. Since 3909269 has no factors of 5, try 7.
8. Removing a factor of 7 yields 558467=3909269/7.
9. Removing a second factor of 7 yields 79781=558467/7.
10. Since 79781 has no factors of 7, try 9.
11. Since 79781 has no factors of 9, try 11.
12. Since 79781 has no factors of 11, try 13.
13. Removing a factor of 13 yields 6137=79781/13.
14. Since 6137 has no factor of 13, try 15.
15. Since 6137 has no factor of 15, try 17.
16. Removing a factor of 17 yields 361=6137/17.
17. Since 361 has no factor of 17, try 19.
18. Removing a factor of 19 yields 19=361/19.
19. Removing a second factor of 19 yields 1=19/19.
20. Since the quotient is already 1, stop and all factors have been reported.
You might feel this is not a very efficient method since testing if 9 and 15 are factors are redundant. Yes, you are right; but, this is already a reasonable complicated program for CS110 and CS201. You could learn more efficient factorization algorithms in other computer science and/or mathematics courses, since this is an extremely important topic.