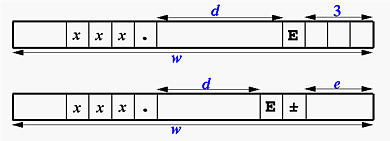
REAL Output: The E Descriptor

The Ew.d and Ew.dEe descriptors are for REAL output. The printed numbers will be in an exponential form. The general form of these descriptors are discussed below. There are two more forms, ESw.d and ENw.d, which will be discussed at the bottom of this page.

rEw.d and rEw.dEe

The meaning of r, w, d and e are:

E is for REAL numbers in exponential forms.
w is the width of field, which indicates that a real number should be printed with w positions.
To print a number in an exponential form, it is first converted to a normalized form s0.xxx...xxx×10^sxx, where s is the sign of the number and the exponent and x is a digit. For example, 12.345, -12.345, 0.00123 and -0.00123 are converted to 0.12345×10², -0.12345×10², 0.123×10^-2 and -0.123×10^-2.
The Ew.d descriptor generates real numbers in the following form:

Of these w positions, the last three are for the exponent, including its sign, the middle d positions are for the number in normalized form. Therefore, excluding the exponent part, there are w-4 positions for printing the digits of the normalized number. In fact, you can consider the normalized number is printed with Fw-4.d. The above figure also includes a 0 and a decimal point. If the number is negative, we must also include its sign. Hence, 4+3=7 positions are not available for printing the normalized number and, as a result, when you use the E edit descriptor, w must be greater than or equal to d+7; otherwise, your number may not be printed properly and all w positions will be filled with asterisks.
The Ew.dEe descriptor generates real numbers in the following form:

As you can see, the only difference is that the exponent part now has e positions. If your data has an exponent larger than 99 or less than -99, Ew.d will not be able to print it properly because there are only two positions for the exponent (therefore, all w positions will be filled with asterisks). As shown in the figure, in addition to the d positions for the normalized number and e positions for the exponent, we need four more positions for printing the sign in the exponent, a decimal point, a leading 0 and the character E. Moreover, if the number is negative, a sign before the 0 is needed. This means that w must be greater than or equal to d+e+5.
r is the repetition indicator, which gives the number of times the edit descriptor should be repeated. For example, 3E20.7E2 is equivalent to E20.7E2, E20.7E2, E20.7E2.

Examples

In the following table, the WRITE statements use different E edit descriptors to print the value of 3.1415926. The WRITE statements are shown in the left and their corresponding output, all using 12 positions, are shown in the right.

The first example uses E12.5 to print 3.1415926. This number is first converted to 0.31415926×10¹. Therefore, the normalized number is 0.31415926 and the exponent is 1. The exponent part is printed as E+01. Since we have only 5 positions for printing 0.31415926 which has 8 digits, the sixth one will be rounded to the fifth and the result is 0.31416.
The second example uses E12.3E4 to print the same number. This E descriptor indicates that four positions are for the exponent and, as a result, the printed exponent part is E+0001.
The last example is obvious. However, if the number is changed to -3.1415926, the result will be 12 asterisks, since there is no position for the sign of the number.

Editor Descriptor ESw.d and ESw.dEe

Scientists write the exponential form in a slightly different way. This ES edit descriptor is for printing a real number in scientific form, which has a non-zero digit as the integral part. If the number is a zero, then all digits printed will be zero. The following shows the printed form:

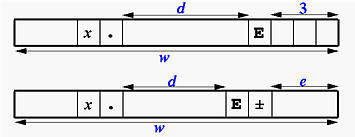
If you understand the form of normalized number, you can just shift the decimal point to the right one position and decrease the exponent by one. The result is in scientific form.

For example, if the number is 34.5678, it has a normalized form 0.345678×10². Now shifting the decimal point to the right one position gives 3.45678×10¹. The following shows the output printed with ES12.3E3:

Editor Descriptor ENw.d and ENw.dEe

Engineers write the exponential form in yet another way. In an engineering form, the exponent is always a multiple of three, and the printed number always has no more than three and at least one non-zero digits. For example, suppose the given number is 1234.567. The integral part has four digits and the exponent is zero. To convert this number to an engineering form, the decimal point should be shifted to the left three positions. Thus, the given number has a new form 1.234567×10³. Similarly, if the given number is 0.00001234567, shifting the decimal point to the right three positions gives 0.01234567×10^-3. However, this is not yet in the engineering form, because the integral part is still zero. Therefore, we need to shift the decimal point to the right three positions again and this gives 12.34567×10^-6. Now, the number is in engineering form.

The following shows the output of ENw.d and ENw.dEe. For ENw.d, it requires 4 positions for the exponent, d positions for the fractional part of the number, 3 positions for the integral part, one position for the decimal point, and one position for the possible sign. It requires at least d+9 positions and consequently for ENw.d, w must be larger than or equal to d+9. The same counting yields that for ENw.dEe, w must be larger than or equal to d+e+7 .