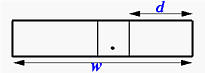
The Fw.d descriptor is for REAL output. The general form is:
The meaning of r, w and d are:

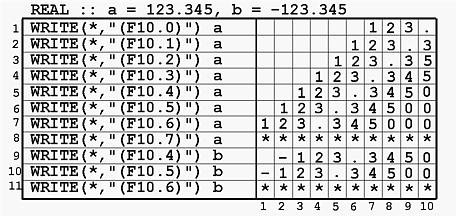
The edit descriptor is 3F6.2 and the format is equivalent to (F6.2,F6.2,F6.2) because the repetition indicator is 3. Therefore, each of these three REAL variables is printed with F6.2. Based on the discussion earlier, the result is the following:REAL :: a = 12.34, b = -0.945, c = 100.0 WRITE(*,"(3F6.2)") a, b, c
