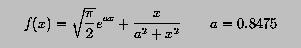
Given a continuous equation f(x)=0 and two values a and b (a < b), if f(a)*f(b) < 0 (i.e., f(a) and f(b) have opposite signs), it can be proved that there exists a root of f(x)=0 between a and b. More precisely, there exists a c, a <= c <= b, such that f(c)=0 holds.
This result provides us with a method for solving equations. If we take the midpoint of a and b, c=(a+b)/2, and computes its function value f(c), we have the following cases:
Your function Funct() is given below:
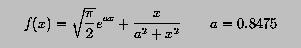
This function has a root near -0.89.
Since this process keeps dividing the intervals into two equal halves,
it is usually referred to as the bisection method. It is also
known as Bozano's method.
![]()
! --------------------------------------------------------------------
! This program solves equations with the Bisection Method. Given
! a function f(x) = 0. The bisection method starts with two values,
! a and b such that f(a) and f(b) have opposite signs. That is,
! f(a)*f(b) < 0. Then, it is guaranteed that f(x)=0 has a root in
! the range of a and b. This program reads in a and b (Left and Right
! in this program) and find the root in [a,b].
! In the following, function f() is REAL FUNCTION Funct() and
! solve() is the function for solving the equation.
! --------------------------------------------------------------------
PROGRAM Bisection
IMPLICIT NONE
REAL, PARAMETER :: Tolerance = 0.00001
REAL :: Left, fLeft
REAL :: Right, fRight
REAL :: Root
WRITE(*,*) 'This program can solves equation F(x) = 0'
WRITE(*,*) 'Please enter two values Left and Right such that '
WRITE(*,*) 'F(Left) and F(Right) have opposite signs.'
WRITE(*,*)
WRITE(*,*) 'Left and Right please --> '
READ(*,*) Left, Right ! read in Left and Right
fLeft = Funct(Left) ! compute their function values
fRight = Funct(Right)
WRITE(*,*)
WRITE(*,*) 'Left = ', Left, ' f(Left) = ', fLeft
WRITE(*,*) 'Right = ', Right, ' f(Right) = ', fRight
WRITE(*,*)
IF (fLeft*fRight > 0.0) THEN
WRITE(*,*) '*** ERROR: f(Left)*f(Right) must be negative ***'
ELSE
Root = Solve(Left, Right, Tolerance)
WRITE(*,*) 'A root is ', Root
END IF
CONTAINS
! --------------------------------------------------------------------
! REAL FUNCTION Funct()
! This is for function f(x). It takes a REAL formal argument and
! returns the value of f() at x. The following is sample function
! with a root in the range of -10.0 and 0.0. You can change the
! expression with your own function.
! --------------------------------------------------------------------
REAL FUNCTION Funct(x)
IMPLICIT NONE
REAL, INTENT(IN) :: x
REAL, PARAMETER :: PI = 3.1415926
REAL, PARAMETER :: a = 0.8475
Funct = SQRT(PI/2.0)*EXP(a*x) + x/(a*a + x*x)
END FUNCTION Funct
! --------------------------------------------------------------------
! REAL FUNCTION Solve()
! This function takes Left - the left end, Right - the right end,
! and Tolerance - a tolerance value such that f(Left)*f(Right) < 0
! and find a root in the range of Left and Right.
! This function works as follows. Because of INTENT(IN), this
! function cannot change the values of Left and Right and therefore
! the values of Left and Right are saved to a and b.
! Then, the middle point c=(a+b)/2 and its function value f(c)
! is computed. If f(a)*f(c) < 0, then a root is in [a,c]; otherwise,
! a root is in [c,b]. In the former case, replacing b and f(b) with
! c and f(c), we still maintain that a root in [a,b]. In the latter,
! replacing a and f(a) with c and f(c) will keep a root in [a,b].
! This process will continue until |f(c)| is less than Tolerance and
! hence c can be considered as a root.
! --------------------------------------------------------------------
REAL FUNCTION Solve(Left, Right, Tolerance)
IMPLICIT NONE
REAL, INTENT(IN) :: Left, Right, Tolerance
REAL :: a, Fa, b, Fb, c, Fc
a = Left ! save Left and Right
b = Right
Fa = Funct(a) ! compute the function values
Fb = Funct(b)
IF (ABS(Fa) < Tolerance) THEN ! if f(a) is already small
Solve = a ! then a is a root
ELSE IF (ABS(Fb) < Tolerance) THEN ! is f(b) is small
Solve = b ! then b is a root
ELSE ! otherwise,
DO ! iterate ....
c = (a + b)/2.0 ! compute the middle point
Fc = Funct(c) ! and its function value
IF (ABS(Fc) < Tolerance) THEN ! is it very small?
Solve = c ! yes, c is a root
EXIT
ELSE IF (Fa*Fc < 0.0) THEN ! do f(a)*f(c) < 0 ?
b = c ! replace b with c
Fb = Fc ! and f(b) with f(c)
ELSE ! then f(c)*f(b) < 0 holds
a = c ! replace a with c
Fa = Fc ! and f(a) with f(c)
END IF
END DO ! go back and do it again
END IF
END FUNCTION Solve
END PROGRAM Bisection
Click here to download this program.
The following output shows that the function values of the input do not have opposite signs and hence program stops.This program solves equation F(x) = 0 Please enter two values Left and Right such that F(Left) and F(Right) have opposite signs. Left and Right please --> -10.0 0.0 Left = -10. f(Left) = -9.902540594E-2 Right = 0.E+0 f(Right) = 1.25331414 A root is -0.89050293
This program solves equation F(x) = 0 Please enter two values Left and Right such that F(Left) and F(Right) have opposite signs. Left and Right please --> -10.0 -1.0 Left = -10. f(Left) = -9.902540594E-2 Right = -1. f(Right) = -4.495930672E-2 *** ERROR: f(Left)*f(Right) must be negative ***