Computing Square Roots with Newton's Method

Problem Statement

We have discussed Newton's Method for computing the square root of a positive number. Let the given number be b and let x be a rough guess of the square root of b. Newton's method suggests that a better guess, New x can be computed as follows:

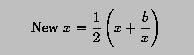
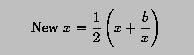
One can start with b as a rough guess and compute New x; from New x, one can generate a even better guess, until two successive guesses are very close. Either one could be considered as the square root of b.

Write a function MySqrt() that accepts a formal argument and uses Newton's method to computes its square root. Then, write a main program that reads in an initial value, a final value, and a step size, and computes the square roots of these successive values with Newton'e method and Fortran's SQRT() function, and determines the absolute error.

Solution

! ---------------------------------------------------------------
! This program contains a function MySqrt() that uses Newton's
! method to find the square root of a positive number.  This is
! an iterative method and the program keeps generating better
! approximation of the square root until two successive
! approximations have a distance less than the specified tolerance.
! ---------------------------------------------------------------

PROGRAM  SquareRoot
   IMPLICIT  NONE

   REAL    :: Begin, End, Step
   REAL    :: x, SQRTx, MySQRTx, Error

   READ(*,*)  Begin, End, Step          ! read in init, final and step
   x = Begin                            ! x starts with the init value
   DO
      IF (x > End)  EXIT                ! exit if x > the final value
      SQRTx   = SQRT(x)                 ! find square root with SQRT()
      MySQRTx = MySqrt(x)               ! do the same with my sqrt()
      Error   = ABS(SQRTx - MySQRTx)    ! compute the absolute error
      WRITE(*,*)  x, SQRTx, MySQRTx, Error   ! display the results
      x = x + Step                      ! move on to the next value
   END DO

CONTAINS

! ---------------------------------------------------------------
! REAL FUNCTION  MySqrt()
!    This function uses Newton's method to compute an approximate
! of a positive number.  If the input value is zero, then zero is
! returned immediately.  For convenience, the absolute value of
! the input is used rather than kill the program when the input
! is negative.
! ---------------------------------------------------------------

   REAL FUNCTION  MySqrt(Input)
      IMPLICIT  NONE
      REAL, INTENT(IN) :: Input
      REAL             :: X, NewX
      REAL, PARAMETER  :: Tolerance = 0.00001

      IF (Input == 0.0) THEN            ! if the input is zero
         MySqrt = 0.0                   !    returns zero
      ELSE                              ! otherwise,
         X = ABS(Input)                 !    use absolute value
         DO                             !    for each iteration
            NewX  = 0.5*(X + Input/X)   !       compute a new approximation
            IF (ABS(X - NewX) < Tolerance)  EXIT  ! if very close, exit
            X = NewX                    !       otherwise, keep the new one
         END DO
         MySqrt = NewX
      END IF
   END FUNCTION  MySqrt

END PROGRAM  SquareRoot

Click here to download this program.

Program Input and Output

If the input values of Begin, End and Step are 0.0, 10.0 and 0.5, the following is the output from the above program.

0.E+0,  0.E+0,  0.E+0,  0.E+0
0.5,  0.707106769,  0.707106769,  0.E+0
1.,  1.,  1.,  0.E+0
1.5,  1.22474492,  1.2247448,  1.192092896E-7
2.,  1.41421354,  1.41421354,  0.E+0
2.5,  1.58113885,  1.58113885,  0.E+0
3.,  1.73205078,  1.7320509,  1.192092896E-7
3.5,  1.87082875,  1.87082863,  1.192092896E-7
4.,  2.,  2.,  0.E+0
4.5,  2.12132025,  2.12132025,  0.E+0
5.,  2.23606801,  2.23606801,  0.E+0
5.5,  2.34520793,  2.34520793,  0.E+0
6.,  2.44948983,  2.44948959,  2.384185791E-7
6.5,  2.54950976,  2.54950976,  0.E+0
7.,  2.64575124,  2.64575148,  2.384185791E-7
7.5,  2.73861289,  2.73861265,  2.384185791E-7
8.,  2.82842708,  2.82842708,  0.E+0
8.5,  2.91547585,  2.91547585,  0.E+0
9.,  3.,  3.,  0.E+0
9.5,  3.08220696,  3.08220696,  0.E+0
10.,  3.1622777,  3.1622777,  0.E+0

Discussion

This program has nothing special. Please refer to the discussion of Newton's method for the computation details of function MySqrt(). However, there is one thing worth to be mentioned. Since the formal argument Input is declared with INTENT(IN), it cannot be changed in function MySqrt(). Therefore, the value of the formal argument Input is copied to X and used in square root computation.