The Curvature Sphere

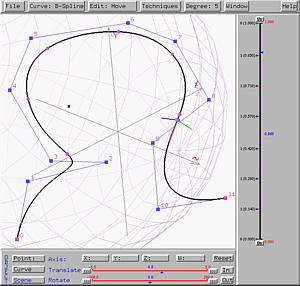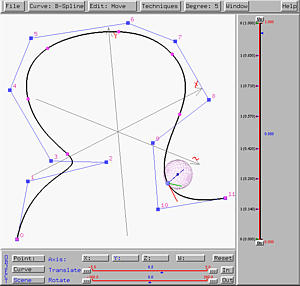
The curvature sphere provides information of the turning rate at a point on the curve. The center of the curvature sphere is always on the positive direction of the normal vector. The curvature at a point on the curve is the reciprocal of the radius of the curvature sphere. As a result, the larger the curvature sphere, the smaller the curvature and the flatter the curve. If a curve has a very sharp turn at a point, the curvature at that point must be very large and the curvature sphere at that point will be very small. On the other hand, if a a curve is flat at a point, the curvature is very small and the curvature sphere will be very larger. Consequently, a straight line has curvature zero because there is no turn on a line, and the curvature sphere will have radius an infinite value at any point on a line. Based on this discussion, it is clear that examining curvature spheres will help you understand if a curve has sharp turns.

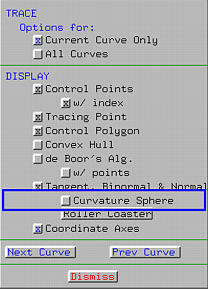
To display curvature sphere, you must first activate Tangent, Binormal & Normal. Once the triad is displayed, click on Curvature Sphere will display the curvature sphere.

The curvature sphere moves according to the movement of the u-indicator. As mentioned earlier, the center of the curvature sphere is on the positive direction of the normal vector, and is displayed as a square. The left figure below shows a curvature sphere. But, when the tracing point moves to the top of the curve which is flat, the curvature sphere becomes bigger indicating the the curve is flat in the vicinity of the tracing point.

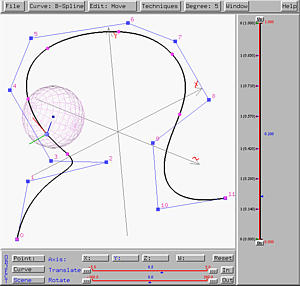
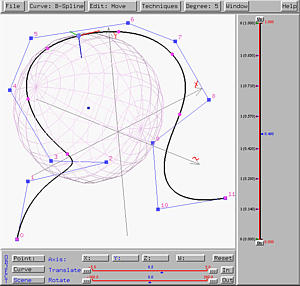
If the tracing point moves further to an inflection point (i.e., a point whose second derivative is zero), the curvature sphere becomes extremely large. Moving pass this inflection point and entering a sharp turn, the curvature sphere is small, meaning that the curvature is large and the curve has a sharp turn there.