Menu Structure: Curve

This menu item is for specifying and displaying curve segments. The supported curve types are Bézier, rational Bézier, B-spline and NURBS curves, where different curve types have slightly different options. Once a curve type is selected, its type is displayed in this item.

New Curve Segment
This item is for specifying the curve type. One of the following four can be selected:
- Bézier
  Bézier curves
- Rational Bézier
  Rational Bézier curves
- B-spline
  B-spline curves
- NURBS
  Non-Uniform Rational B-spline curves
Normally, one should select a curve type followed by creating control points. If control points have already been created on the drawing canvas with a wrong curve type, one can use Change Current Curve to to change the curve type without changing the control points.
Once B-spline or NURBS is selected, this program assumes the curve has degree 3 and displays this degree in the Degree menu. If degree 3 is not suitable for a particular application, it can be changed with the Degree menu. Note that the maximum degree is 10 for B-spline and NURBS curves, which is sufficient for most applications.
Show Curve Segment
If the curve type is Bézier or rational Bézier, this item is unnecessary since the curve will be generated on-the-fly as control points are being created.
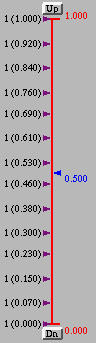
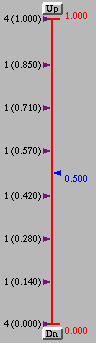
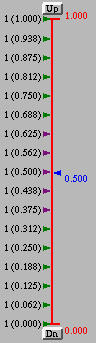
For a B-spline and NURBS curve, it is required to tell this system if the curve should be displayed as an open curve, a clamped curve or a closed curve. These three types of curves correspond to with Uniform Knots, with Clamped Knots and with Closed Knots, respectively.

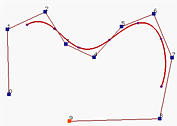
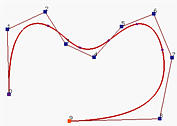
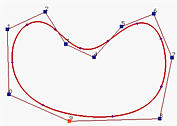
The above figures, from left to right, show open, clamped and closed B-spline curves of degree 4 with the same set of control points. An open B-spline/NURBS curve does not pass though the first and the last control points. This system displays an open B-spline/NURBS curve with uniformly spaced knots. A clamped B-spline/NURBS curve is tangent to the first and last legs at the first and last control points, respectively. This system displays a B-spline/NURBS curve with the first p+1 knots and the last p+1 knots clamped to 0 and 1, respectively. All internal knots are uniformly spaced. For a closed B-spline/NURBS curve, the knots are still uniformly spaced; but some knots at both ends are fixed and cannot be modified.
Note that except for closed B-spline/NURBS curves, one can always manipulate the knot vector to make an open B-spline/NURBS a clamped one and vice versa.
This item can be selected at any time to change its knot pattern after a B-spline and NURBS curves has been displayed.
Change Current Curve to
This item allows a curve on the drawing canvas to be changed to another type using the same set of control points. There are four choices under this item: Bézier, Rational Bézier, B-spline and NURBS. Once one of them is selected, the curve is "converted" to the desired type. Note that this conversion simply "forgets" the original curve type and uses the same set of control points to generate a new one. As a result, when B-spline or NURBS are selected, its degree and its knot pattern (i.e., open, clamped and closed) are required before a curve can be displayed.
Next Curve Segment
Make the next curve the current curve segment. If the current curve segment is the last one, the next curve segment is the first curve.
Previous Curve Segment
Make the previous curve the current curve segment. If the current curve segment is the first one, the previous curve segment is the last curve.

Knot Vector

The left side of the vertical slider in the drawing canvas is used to display the knot vector. The following figures, from left to right, show the knot vectors of an open, a clamped and a closed B-spline curve of degree 4. In the display, a knot is shown as p(q), where q is the knot value and p is its multiplicity. For example, in the knot vector of the open B-spline curve, 1(0.760) means 0.760 is a knot whose multiplicity is 1 (i.e., 0.760 is a simple knot). In the knot vector of the clamped B-spline curve, the clamped knots are 4(0.000) and 4(1.000) which means knots 0 and 1 are of multiplicity 4. For a closed B-spline and NURBS curve, several knots near 0 and 1 are shown in a different color, which means they cannot be modified (i.e., fixed to make the curve closed).