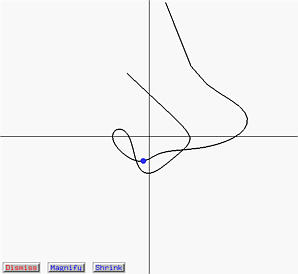
The First Derivative (Hodograph) and Second Derivative Curves

The derivatives of Bézier and B-spline curves are still Bézier and B-spline curves, respectively. In fact, the derivatives of a Bézier (resp., B-spline) curve is a curve defined by a new set of control points that are constructed from the original set of control points. The degree of the derivate curve is, of course, one less than the original. The following figure shows a B-spline curve of degree 5 with tracing point corresponding to u = 0.6.

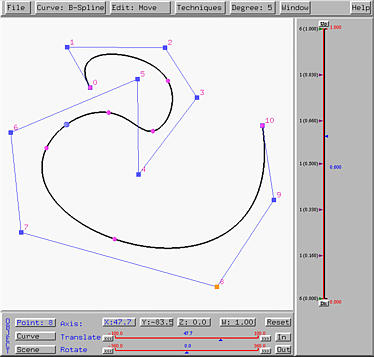
To display the first derivate curve or hodograph, select Window, followed by Hodograph (First Derivative). To display the second derivative curve, select Second Derivative. Then, a new window appears showing the first or second derivate curve in the same type of the current curve on the drawing canvas. The left (resp., right) figure below shows the hodograph (resp., second derivative) curve of the above B-spline curve. As a result, both derivative curves are B-spline curves.

Each of these derivative windows contains three buttons:

  1. Magnify zooms in and makes the derivate curve looks larger.
  2. Shrink zooms out and makes the derivate curve looks smaller.
  3. Dismiss closes the window.
Since the size or range of the curve is usually unpredictable before computation starts, buttons Magnify and Shrink help make the derivative curves fit into the window boundary. Once these derivative windows are shown, moving the u-indicator will not only move the tracing point on the curve, but also the tracing points on each of the two derivative curves.

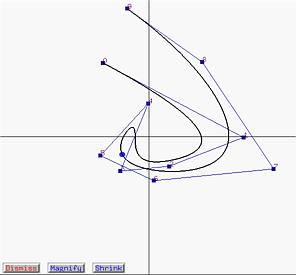
Unfortunately, the derivative curves of a NURBS (and hence a rational Bézier) curve is in general not a curve in one of the four types. As a result, no control points will be shown in the derivative windows. These derivative curves are approximated with line segments. The following figure shows a NURBS curve of degree 5.

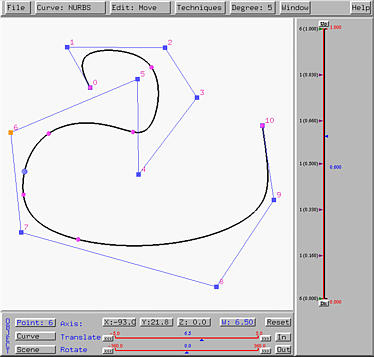
The left (resp., right) figure below shows the hodograph (resp., second derivative) curve. You can see clearly that the curves are made from line segments and no control points are shown.