
There are three ways of modifying the shape of a curve, namely modifying control points, modifying knots, and modifying the weights of control points. The first works for all four types of curves, the second can be applied to B-spline and NURBS curves, and the third can be used with rational Bézier and NURBS curves. This page concentrates on the second one: modifying the knots of a B-spline or a NURBS curve.
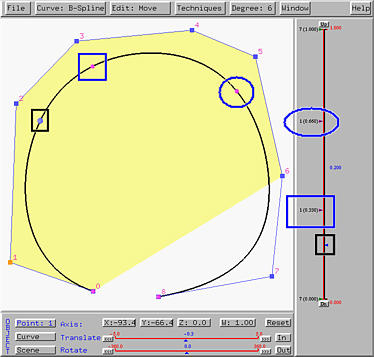
Before discussing knot modification, we need to review the drawing canvas. The vertical slider is for curve tracing and displaying knots and their multiplicities. The small triangle in the right-hand side is referred to as the u-indicator. Dragging the u-indicator up and down moves the corresponding point, the tracing point, on the curve. The figure below shows the u-indicator at u=0.2 and its corresponding point. Both are marked with black rectangles.

The left-hand side of the slider has the knots and their multiplicities. Each knot is displayed in a form of m (d.ddd), where d.ddd is the value of a knot and m is its multiplicity. The positions of knots are marked with little triangles in the left side of the vertical slider. These triangles are called the knot indicators. The figure above has 16 knots. They are 0 (multiplicity 7), 1/3 (simple knot), 2/3 (simple knot), and 1 (multiplicity 7). Knots that are not 0 and 1 are internal knots. Each knot has its corresponding point on the curve, shown as smaller spheres. These are called knot points. In the figure above, knot 1/3 and its corresponding point on the curve are marked with blue rectangles, and knot 2/3 and its corresponding point on the curve are marked with blue ellipses.
Knot points subdivide the curve into curve segments, each of which is a curve of degree the same as the given one. In the figure above, there are three curve segments obtained from the two knot points at both ends (i.e., knot points corresponding to 0 and 1) and two knot points corresponding to the internal knots. Since a knot may be a multiple knot, the number of knot points is always less than or equal to the number of knots.

To change the value of a knot that is not 0 and 1, one can drag the corresponding knot indicator shown in the left-hand side of the vertical slider. As the knot moves, the shape of the curve changes on-the-fly. In the following figure, the value of u is 0.2. If the knot 2/3 is moved to 0.8, the corresponding knot point moves closer to control point 6, and the curve segment between this knot point and the end point becomes shorter (see the left figure below). At the same time, the other knot point moves as well. It moves toward control point 1, making the curve segment between these two knot points longer than the original (see the figure above). The curve segment between the knot point corresponding to 2/3 and the end point has a sharper turn.
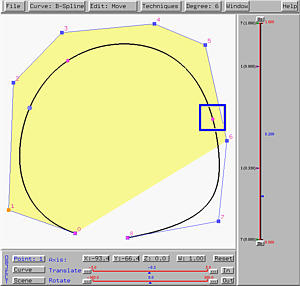
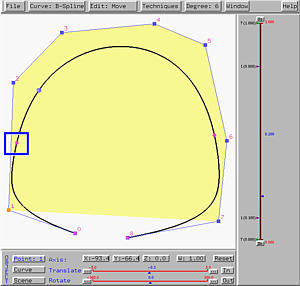
Moving knot 1/3 to 0.1 yields the same effect as described earlier (see the right figure above).

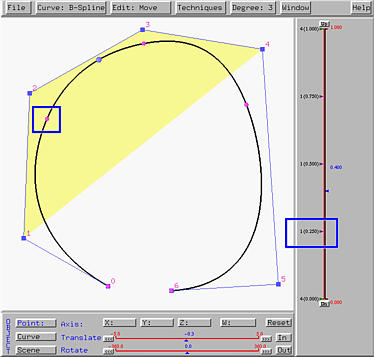
As knot 0.25 moves, you will see the knot points corresponding to 0.25 and 0.5 move toward each other and eventually become the same knot point when knot 0.25 is moved on top of knot 0.5. Moreover, the curve is tangent to the line segment of control point 2 and control point 3 at the knot point corresponding to 0.5. This is shown in the left figure below.
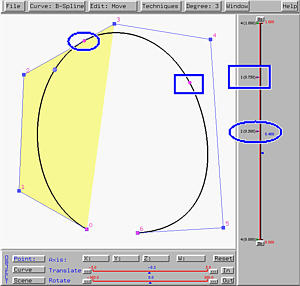
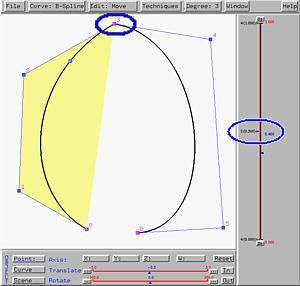
Now, let us move the other knot 0.75 to the new double knot 0.5, making it a triple one. As knot 0.75 moves, the two knot points move toward each other and at the same time move toward control point 3. Once knot 0.75 moves on top of knot 0.5, the two knot points and control point 3 become identical. Moreover, the curve at control point 3, which now corresponds to knot 0.5, is no more smooth (i.e., the tangent vectors at control point 3 of each segment are different. This is shown in the right figure above.
In theory, we know that a B-spline or a NURBS curve at a knot of multiplicity k is of Cp-k continuity, where p is the degree of the curve. Therefore, in the right figure above, the knot point corresponding to triple knot 0.5 is C0. That is, the tangent vectors of the two sides at that knot point are different.
The curve is tangent to a line segment at a knot point, if the multiplicity of the corresponding knot is p-1, where p is the degree of the given B-spline or NURBS curve. Note that the curve is of C1 continuity at that knot point (i.e., the tangent vectors at that point of the curve segments are equal). The line segment to which the curve is tangent depends on the location of the knot and is determined using the convex hull property. As a result, in the left figure above, since 0.5 is a double knot and the curve is of degree 3, the curve is tangent to a line segment of the control polygon.