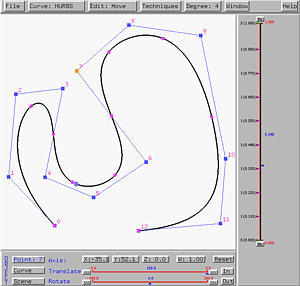
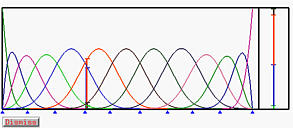

The Partition of Unity Window displays the partition of unity of a curve and its basis functions. The left figure below shows a clamped B-spline curve of degree 4. The right figure below is its partition of unity window. The small triangles show the position of knots. As u changes, a vertical bar also moves in this partition of unity window. The values of basis functions are stacked up as shown with fixed vertical bar in the right side of the window. Different basis functions are shown in different colors. Thus, the fixed vertical bar is "partitioned" by different color intervals and this is the way of partitioning [0,1] at u. Note that as u changes, the partition changes as well.


If the knot vector is modified, the partition of unity changes on-the-fly, reflecting the change being made with the knot vector. The following figures show the result of merging some knots into multiple knots. The new knot vector has the same end knots, but the internal knots are 0.25(2), 0.5(3) and 0.75(3). That is, some of the knots are combined to create multiple knots: 0.25 with multiplicity 2 and 0.5 and 0.75 with multiplicity 3. Please note the change of knot positions in the partition of unity window.
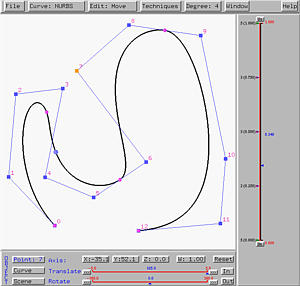
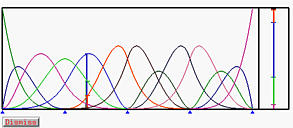
Please also note that before merging knots a basis function is non-zero on five knot spans. After merging knots, some basis functions are non-zero on only one knot span. In general, none of the basis functions is non-zero on more than two knot spans.