
There are three ways of modifying the shape of a curve, namely modifying control points, modifying knots, and modifying the weights of control points. The first works for all four types of curves, the second can be applied to B-spline and NURBS curves, and the third can be used with rational Bézier and NURBS curves. This page concentrates on the third one: modifying the weights of control points.
Since only rational Bézier and NURBS curves allow control points to have weights, modifying weights can only be used with these two types of curves. To modify the weight of a control point, this control point must be selected first. If the system is in the move mode, clicking on a control point selects it. Otherwise, one can enter the move (resp., select) mode by selecting Edit followed by Move (resp., Select). Then, clicking on a control point selects it.
After selecting a control point, its color changes and its coordinates and weight will be displayed in the four buttons near the bottom of the drawing canvas. Clicking on W selects changing weight. The button color will change to blue meaning that W is selected for further editing. Finally, use the Translate slider below the W button to adjust the value of the selected weight. As the weight changes, the shape of the curve changes on-the-fly.
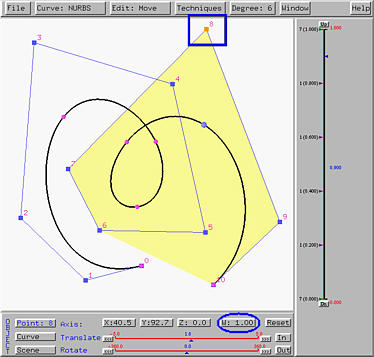
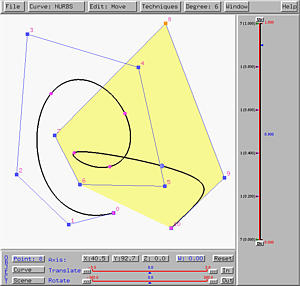
Let us take a look at an example. The following shows a NURBS curve of degree 6 with control point 8 selected.

Now, click on W to select weight. Then, increase its value to 3 with the Translate slider. The curve will be pulled toward the selected control point. This is shown in the left figure below. If the weight is further increased to 10, the curve will be pulled further toward the selected control point. In fact, increasing the weight of a control point pulls the curve toward that control point. Moreover, if the weight is increased to infinity, the curve passed through the selected control point.
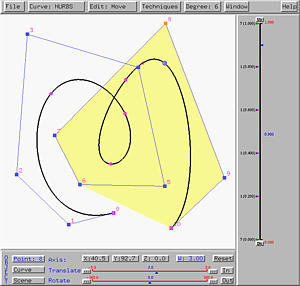
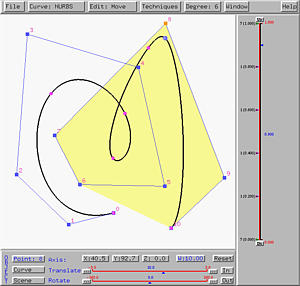
Let us decrease the weight to 0.5. The curve is pushed away from the selected control point as shown in the left figure below. If the weight is decreased further, the curve is pushed further away. The right figure below has the weight decreased to 0.1. Decreasing the weight of control point pushes the curve away from that control point..
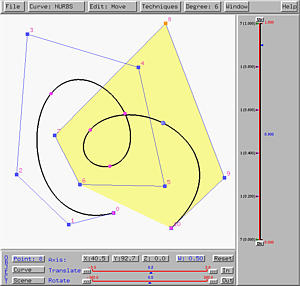

What if the weight is changed to zero? This removes the impact of the selected control point. The left figure below has weight zero for control point 8. The affected part of the curve becomes flat meaning that the influence of control point 8 disappears. If the weight decreases further becoming a negative value, the curve will move further away from the selected control point as shown in the right figure below. In this case, the curve segment moves outside of its convex hull, violating the convex hull property.

The convex hull property help us determine the bound of a curve segment. This can be achieved only if the weights of control points are all non-negative. As a result, even though this system supports negative weights (the right figure above), it is usually unwise to use them.