Simple Shapes

POVRAY supports several simple objects: spheres, boxes, planes, cylinders, cones and tori:

sphere { < a, b, c >, r }
plane  { < a, b, c >, d }
box { < p, q, r >, < u, v, w > }
cylinder { < p, q, r >, < u, v, w >, R [open] }
cone { < p, q, r >, R1, < u, v, w >, R2 [open] }
torus { R1, R2 }

Spheres

A sphere is defined by its center < a, b, c > and radius r:

sphere { < a, b, c >, r }

Thus, a sphere with center < 0, 0, 0 > and radius 1 is written as

sphere { < 0, 0, 0 >, 1 }

sphere {
     0*x,  1
}

Planes

A plane is defined by its normal vector < a, b, c > and the distance d from the origin to this plane:

plane  { < a, b, c >, d }

Note that a normal vector always points outward. That is, normal vectors always point to the exterior of the surface. The distance d is measured from the origin to the plane. If the direction from the origin to this plane is identical to that of the normal vector, the distance is positive; otherwise, it is negative.

For example, suppose we have a plane like

plane { x+y+z, 1.141 }

Its normal vector is < 1, 1, 1 > and the distance from the origin to this plane is 1.414 (the square root of 2). Since the distance is positive, it is considered in the same direction as the normal vector. As a result, the plane is the one containing the green triangle (the plane is clipped to show the other one). If the plane is changed to

plane { x+y+z, -1.141 }

Since the distance is negative and is in the opposite direction of the normal, the resulting plane is the one containing the other triangle.

Boxes

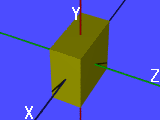
A box can be completely defined by two opposite vertices. In the following, <p, q, r> and <u, v, w> are the lower-left and upper-right corners.

box { < p, q, r >, < u, v, w > }

If a box is defined as

box {
     < -1, -1, -0.5 >,    // lower-left corner
     <  1,  1,  0.5 >     // upper-right corner
}

in the x-, y- and z-axis direction, the widths of the box are 2, 2 and 1. Here is the result:

Cylinders

A cylinder is defined by two points and a radius. If open is selected, the cylinder does not have caps, that is, it is a open tube. The line that contains the given points is the axis of the cylinder and the two caps, which are circles with centers the given points, lie on planes perpendicular to the axis. In the following, < p, q, r> and < u, v, q> are the centers of the cap circles and R is the radius.

cylinder { < p, q, r >, < u, v, w >, R [open] }

The following figure shows two cylinders. The left one does not have keyword open specified and hence two caps are added, one on the top and the other on the bottom. The figure also shows the axis of the cylinder. The red spheres are the given points. Both the axes and points are shown for illustration purpose and should not appear in the image.

Cones

A cylinder is a special case of a cone. If the radii of the top and bottom circles are different, we have a cone. In the following < p, q, r > and R1 are the center and radius of a cap circle, while < u, v, w > and R2 are the center and radius of another cap circle. Like cylinder, you can add open to remove the cap circles.

cone { < p, q, r >, R1, < u, v, w >, R2 [open] }

Below are two cones, the left is a closed one. Again, the axes and points (i.e., red dots) are shown to you for illustration purpose. Both should not appear in your image.

Tori

Torus can be defined as the result of revolving a circle about a line. The center of the revolving circle lies on another circle, which is usually referred to as the major circle and its radius the major radius. The revolving circle itself is referred to as the minor circle and its radius minor radius.

In POVRAY, the line is the y-axis. The major circle has its center at the origin and radius R1. The plane that contains the minor circle passes through the y-axis. The minor circle has its center on the major circle and its radius R2. Thus, POVRAY puts a torus in a very special position so that a torus can be defined only with a major radius and a minor radius as follow:

torus { R1, R2 }

The following figure is generated with major radius 1 and minor radius 0.5.

torus { 1, 0.5 }

The left figure shows the major and minor circles, and the coordinate axes, while the right one shows the generated torus. Note that the coordinate axes are not parts of the torus.