Geometric Transformations

A shape can be translated, rotated and scaled. These are called geometric transformations. In POVRAY, geometric transformations are specified as follows:

translate  < a, b, c >
rotate     < a, b, c >
scale      < a, b, c >
scale      s

translate will translate the shape in the direction of < a, b, c >. More precisely, if a point on the shape has a coordinate < p, q, r >, then translate < a, b, c > brings that point to < p+a, q+b, r+c >.

scale has two forms. In fact, the second form is equivalent to scale < s, s, s > and is a special case of the first. scale < a, b, c > scales the x, y and z coordinate by factors a, b and c, respectively. More precisely, if < p, q, r > is a point of the shape, after scaling, this point becomes < p*a, q*b, r*c >.

rotate is more complicated. First, please keep in mind that POVRAY uses a left-handed coordinate system. Consequently, the positive direction for angle measuring is different from what you learn in a geometry course. Try to do the following to understand the positive direction:

Hold a coordinate axis with your thumb pointing in the positive direction. Then, your other four figures point to the positive direction for angle measure.

Second, POVRAY uses degree for angle measure rather than radian. In rotate < a, b, c >, it means rotating the shape about the x-axis a degree, followed by rotating the resulting shape about the y-axis b degree, followed by rotating the resulting shape about the z-axis c degree. Therefore, rotate < a, b, c > is equivalent to executing the following rotations in order:

rotate  a*x      or     rotate < a, 0, 0 >
rotate  b*y      or     rotate < 0, b, 0 >
rotate  c*z      or     rotate < 0, 0, c >

If you want to fine tune your rotations, the above form could be more helpful than rotate < a, b, c >.

Using Geometric Transforms in a Shape

You can apply as many transformations in any order as you want to a shape. Just add the desired transformations to the shape specification. For example, the following box is first translated to < 4, 5, 6.5 >, rotated about the x-axis 30 degree, scaled in the x-, y- and z-direction using factors 1, 2 and 0.5 respectively, translated again to < -1, 0, 0 >, and finally rotated about the y-axis 50 degree.

box {
     < -1, -1, -1 >, < 1, 1, 1 >
     translate   < 4, 5, 6.5 >
     rotate      30*x
     scale       < 1, 2, 0.5 >
     translate   < -1, 0, 0 >
     rotate      < 0, 50, 0 >
}

Consider a cylinder whose axis is the z-axis:

cylinder { -z, z, 1 open }

The following figure is generated using translate and scale:

The left-most shape in the above figure is generated with

cylinder {
     -z, z, 1 open
     scale      < 1, 0.25, 1 >
     translate  < 3, 0, 0 >
}

The cylinder is first "scaled" in the y-direction and translated to < 3, 0, 0 >. Therefore, the circular cap becomes a thin ellipse.

The second shape is generated with

cylinder {
     -z, z, 1 open
     scale      < 1, 0.5, 1 >
     translate  < 1, 0, 0 >
}

The cylinder is scaled in the y-direction and translated to < 1, 0, 0>. The third one is scaled with scale < 1, 0.75, 1> and then translate < -1, 0, 0 >. The fourth one is not scaled but translated with translate < -3, 0, 0 >.

If you do not want to scale a shape in a direction, use 1 for that direction as shown in the above example. You cannot use 0.

The following figure shows the effect of rotation. The yellow box is the given one. Rotating it about the x-axis -60 degree yields the cyan box, while rotating the given box about the x-axis 60 degree gives the magenta box. This illustrates the difference of using a left-handed coordinate system.

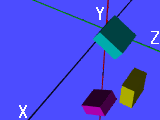
Rotations are not commutative. The following figure is a good example.

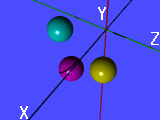
The yellow sphere is the given one defined by the following:

sphere { < 2, 0, 1 >, 0.5 }

The cyan sphere is obtained from the given one by first rotating about the x-axis -60 degree and then rotating the resulting shape about the y-axis 45 degree:

sphere { 
     < 2, 0, 1 >, 0.5 
     rotate  -60*x
     rotate  45*y
}

The magenta sphere is obtained from the given one by first rotating about the y-axis 45 degree and then rotating the resulting shape about the x-axis -60 degree.

sphere { 
     < 2, 0, 1 >, 0.5 
     rotate  45*y
     rotate  -60*x
}

As you can see from the figure that the cyan sphere and the magenta sphere are not the same one. Therefore, rotations are not commutative.