Triangles and Smooth Triangles

Since surfaces are frequently subdivided into triangles, raytracing a group of triangles is a common practice, although it is usually very slow. Two types of triangles are supported by POVRAY, namely triangle {} and smooth_triangle {}. Since triangles and smooth triangles do not have inside and outside (i.e., interior and exterior), they cannot be used with Boolean operations intersection and difference; but, they can be used with union for simplifying modeling process.

Syntax

The syntax rules for triangle {} and smooth_triangle {} are

triangle {
     vertex-1,          // in vector form
     vertex-2,          // in vector form
     vertex-3           // in vector form
     // other specifications such as pigment, finish, ...
}

smooth_triangle {
     vertex-1, normal-1,
     vertex-2, normal-2,
     vertex-3, normal-3
     // other specifications
}

Both forms require three vectors indicating the vertices of a triangle; but the smooth triangle also requires the normal vector at each vertex. Note that the normal vector does not have to be the true normal vector at that vertex. This is because in many cases the true normal vector is not available and must be approximated. Moreover, this normal vector is for rendering purpose and as a result one can use an arbitrary vector for generating special effect. The reason of using smooth_triangle {} is for rendering purpose. With a normal vector at each vertex, POVRAY is able to interpolate a color for each pixel so that the resulting triangle looks smooth (i.e., part of a curvilinear surface).

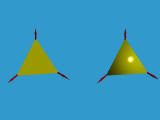
The above left triangle is generated with vertices < 1, 0, 0 >, < 0, 1, 0 > and < 0, 0, 1 >:

triangle {
     x, y, z
}

while the above right triangle is generated with

smooth_triangle {
     x, x,
     y, y,
     z, z
}

where vertices x, y and z have normal vectors x, y and z, respectively. Note that this triangle looks smooth although it is actually flat.

Example I

A typical use of triangle {} and smooth_triangle {} is to display a "triangulated" surface. Many surfaces are very difficult to display or visualize. One way to overcome this problem is to subdivide the surface into many triangles. If the normal vector at each vertex can be calculated, smooth_triangle {} can be used to display the original surface. If normal vectors are not available, one can either compute an approximated normal vector at each vertex or just use triangle {}. The former can still generate a curvilinear surface; but its shading may have some distortion since normal vectors are not completely correct. The latter case can only generate a polyhedron which does not look smooth.

If the parametric equation of a surface is given, generating triangles would be very easy. For example, if the domain is a rectangle [a,b] x [c,d]. Then, one can subdivide [a, b] into m segments a₀=a, a₁, ..., a_m=b and subdivide [c, d] into n segments c₀=c, c₁, ..., c_n=d. Thus, for each rectangle defined by four neighboring points in the domain, a_i, a_i+1, c_i and c_i+1, we have two triangles with vertices (a_i,c_i), (a_i+1,c_i) and (a_i,c_i+1) and (a_i,c_i+1), (a_i+1,c_i+1) and (a_i+1,c_i). These triangles in the domain are mapped to the surface by the parametric equations becoming triangles on the surface. Note that only the vertices of these triangles lie on the surface and the triangles themselves are not. But, at least, one can generate the vertices and normal vectors for raytracing.

A sphere has the following parametric equation:

f(u,v) = ( a + rcos(u)cos(v), b + rsin(u)cos(v), c + rsin(v) )

where (a, b, c) and r are the center and radius and both parameters u and v are in the range of 0 and 2*PI.

The above figures show the effects of different numbers of subdivisions. Each figure contains three spheres. The left one is given by sphere { < 0, 0, 0 >, 1 }, the middle one uses smooth_triangle {} and the right one uses triangle {}. The first figure shows two subdivisions in each direction. More precisely, [0,2*PI] is subdivided into [0,PI] and [PI,2*PI]. Therefore, the domain [0,2*PI] x [0, 2*PI] is subdivided into four smaller squares each of which is further subdivided into two triangles. Therefore, there are eight triangles in total. As you can see from the figure, both smooth_triangle {} and triangle {} do not look like spheres.

The next figure shows the effect of subdividing the domain into 16 squares and hence 32 triangles. The third one has 32 squares and hence 64 triangles. The fourth one has 64 squares and hence 128 triangles. Even with 128 triangles, the green "sphere" that is generated with triangle {} is not yet a sphere. But the yellow one that is generated with smooth_triangle {} looks very smooth and close to a sphere.

Note that these triangles are generated by a C program which outputs a union like the following:

//   Polygonalized smooth sphere with 16 subdivisions

#declare  SMOOTH_TRIANGLE =
union {
   smooth_triangle {
      < 0.000000, 1.000000, 0.000000 >, < 0.000000, 1.000000, 0.000000 >,
      < 0.382683, 0.923880, 0.000000 >, < 0.382683, 0.923880, 0.000000 >,
      < 0.353553, 0.923880, 0.146447 >, < 0.353553, 0.923880, 0.146447 >
   }
   smooth_triangle {
      < 0.000000, 1.000000, 0.000000 >, < 0.000000, 1.000000, 0.000000 >,
      < 0.353553, 0.923880, 0.146447 >, < 0.353553, 0.923880, 0.146447 >,
      < 0.270598, 0.923880, 0.270598 >, < 0.270598, 0.923880, 0.270598 >
   }
   smooth_triangle {
      < 0.000000, 1.000000, 0.000000 >, < 0.000000, 1.000000, 0.000000 >,
      < 0.270598, 0.923880, 0.270598 >, < 0.270598, 0.923880, 0.270598 >,
      < 0.146447, 0.923880, 0.353553 >, < 0.146447, 0.923880, 0.353553 >
   }

     // other smooth triangles

   smooth_triangle {
      < 0.000000, -1.000000, 0.000000 >, < 0.000000, -1.000000, 0.000000 >,
      < 0.353553, -0.923880, -0.146447 >, < 0.353553, -0.923880, -0.146447 >,
      < 0.382683, -0.923880, 0.000000 >, < 0.382683, -0.923880, 0.000000 >
   }
}

Example II

Consider one more example. The following is an "elliptical" torus:

f(u,v) = ( (a + bcos(v))cos(u), csin(v), (a + bcos(v))sin(u) )

where u and v are in the range of 0 and 2*PI and a = 8, b = 3 and c = 7. This surface is generated by revolving an ellipse about the y-axis. The following figure is rendered with smooth triangles by subdividing both directions into 20 segments and hence the domain [0,2PI] x [0,2PI] into 400 squares (800 triangles).

A typical way of generating these triangles is done with a function similar to the following:

void  GridGen(void)
{
     POINT3D *r;
     NORM3D  *n;
     int     j;

     r1 = Row1;
     n1 = Norm1;
     r2 = Row2;
     n2 = Norm2;
     u  = u1;
     OneRow(r1, n1);
     for (u = u1+DeltaU; u <= u2; u += DeltaU) {
          OneRow(r2, n2);
          for (v = v1, j = 0; v < v2; j++, v += DeltaV) {
               SmoothTriangle(r1[j], r2[j], r1[j+1], n1[j], n2[j], n1[j+1]);
               SmoothTriangle(r2[j], r1[j+1], r2[j+1], n2[j], n1[j+1], n2[j+1]);
          }
          SWAP(r1, r2, r);
          SWAP(n1, n2, n);
     }
}

Each call to SmoothTriangle() outputs a smooth triangle. Function OneRow() prepares one row of division points for triangle generation. To see the complete detail, please click here to download a copy of this file. The following is part of the the output from this program. You can save this output to a file and then #include it into the scene file.

#declare  TRIANGULATED_TORUS =
     union {
          smooth_triangle {
               < 11.000000, 0.000000, 0.000000 >, < -1.000000, 0.000000, 0.000000 >,
               < 10.461622, 0.000000, 3.399187 >, < -0.951057, 0.000000, -0.309017 >,
               < 10.853170, 2.163119, 0.000000 >, < -0.990443, -0.137921, 0.000000 >
          }
          smooth_triangle {
               < 10.461622, 0.000000, 3.399187 >, < -0.951057, 0.000000, -0.309017 >,
               < 10.853170, 2.163119, 0.000000 >, < -0.990443, -0.137921, 0.000000 >,
               < 10.321978, 2.163119, 3.353814 >, < -0.941968, -0.137921, -0.306064 >
          }
               // other smooth triangles
          smooth_triangle {
               < 10.853170, -2.163119, 0.000000 >, < -0.990443, 0.137921, 0.000000 >,
               < 10.461622, 0.000000, -3.399187 >, < -0.951057, 0.000000, 0.309017 >,
               < 11.000000, 0.000000, 0.000000 >, < -1.000000, 0.000000, 0.000000 >
          }
     }