
Degree elevation is one of the several fundamental geometric algorithms that permit to modify the defining parameters of a surface without changing its shape. Due to the fundamental identity (i.e., m = n + p + 1, where m+1, n+1, and p are the number of knots, the number of control points, and the degree of a B-spline or a NURBS curve), increasing the degree of a curve by 1 requires a modification to the control points and knot vector. One can increase the degree of a Bézier curve easily. For a B-spline or a NURBS curve, one can subdivide the curve into Bézier curve segments, increase the degrees of these Bézier curves, and combine them back to a B-spline or a NURBS curve. In this process, the original set of control points and knot vector are replaced by the new ones.
For a surface, one can degree elevate in either the u- or the v- direction. In this case, every row or column of control points will be modified by the curve elevation algorithm for curves.
We shall use a NURBS surface defined by 6 rows and 6 columns of control points and degrees 4 and 3 in the u-direction and the v-direction, respectively. You can click here to download a copy of this file deg-elev.dat for your practice.
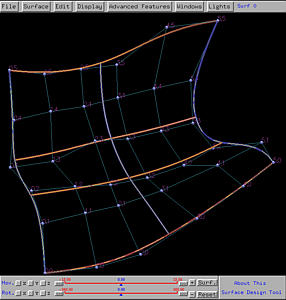
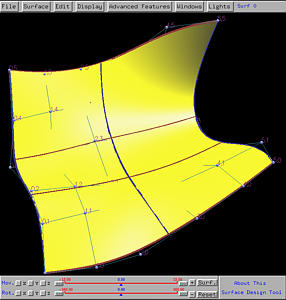
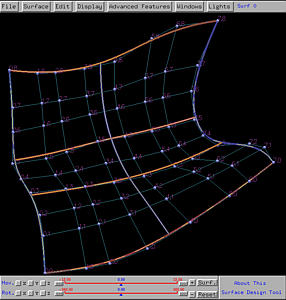
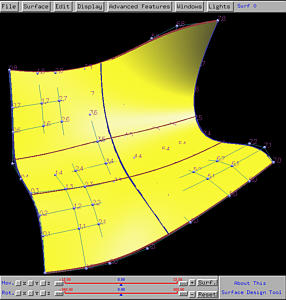
To show the impact on the control points, the surfaces will be displayed using Display, followed by Rendering Method, followed by Wireframe, followed by Detail Level 1. The knot curves are also shown. Note that the knot distribution in the u-direction is 0 (multiplicity 5), 0.5 (simple) and 1 (multiplicity 5), and the knot distribution in the v-direction is 0 (multiplicity 4), 1/3 (simple), 2/3 (simple), and 1 (multiplicity 4). The following is the initial surface, shown in wireframe and rendered patch.


Let us increase the degree by one in the u-direction. Select Advanced Features, followed by Degree Elevation, followed by on U. The result is shown below. As you can see the shape of the surface does not change, and each "row" of the original control points is replaced by a set of new control point. Now there still are 6 rows; but, the number of columns (i.e., the number of control points on each row) increases to 8 from 6.
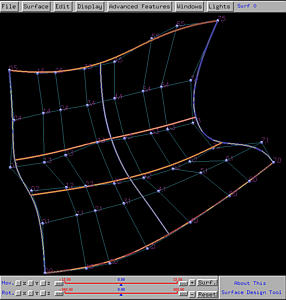
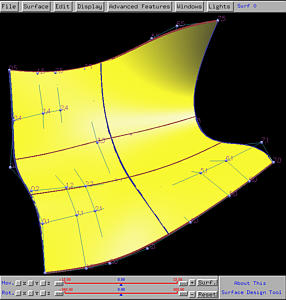
Let us increase the degree by one in the v-direction. Select Advanced Features, followed by Degree Elevation, followed by on V. The following figures show the result. The number of columns is the same (i.e., 8); but, the number of rows (i.e., the number of control points on each column) increases to 9 from 6.
Please check the change of the number of knots in each direction, and verify the fundamental identity. You can get the number of knot information from the Tracing Window.