

To modify the shape of a surface, one can change the position of control points, and remove a row or a column of control points. If the surface is a rational Bézier or a NURBS surface, one can change the weight of a control point. If the surface is a B-spline or a NURBS, one can also change the positions of knots. Note that one cannot add control points; but, one can add knots by knot insertion without changing the shape of the surface. This page focuses on moving knots.

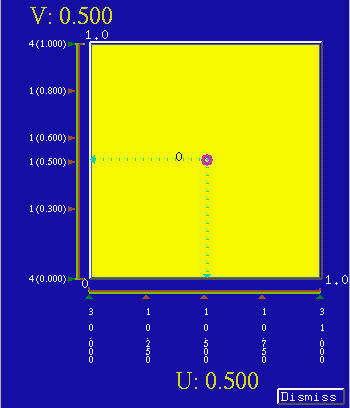
B-spline and NURBS surfaces involve knots. Information about knots are shown in the Tracing Window. In the following figure, the horizontal direction is the u-direction and the vertical direction is the v-direction. All knots are marked with little triangles. For each knot, there are two numbers, its multiplicity and the knot value. For the knots in the u-direction, the top number is the multiplicity and the number below the multiplicity is the knot value. Thus, the figure shows that the u-direction has nine knots: (1) 0 is a knot of multiplicity 3, (2) 0.25, 0.5 and 0.75 are simple knots, and (3) 1 is a knot of multiplicity 3. For the knots in the v-direction, the number in a parenthesis is the knot value, while the multiplicity is shown to the left of the knot value. Therefore, in the v-direction, there are 12 knots: (1) 0 is a knot of multiplicity 4, (2) 0.3, 0.5, 0.6 and 0.8 are simple knots, and (3) 1 is a knot of multiplicity 4. Click here to download file knot.dat for your practice.
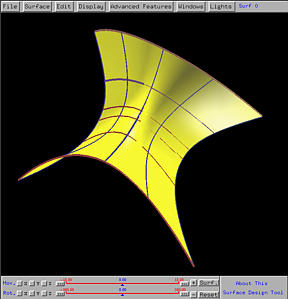
Suppose a surface is denoted as S(u,v). Then, fixing a knot value ui in the u-direction or vj in the v-direction, the curve S(ui,v) is an isoparametric curve in the u-direction, and the curve S(u, vj) is an isoparametric curve in the v-direction. Since these isoparametric curves correspond to knot values, they are referred to as knot curve. To display knot curves on the surface, select Display followed by Show Knot Curves. The following is an example. Since there are five knots in the u-direction, there are five knot curves in the vertical (i.e., v) direction. Of these five, two are boundary curves.
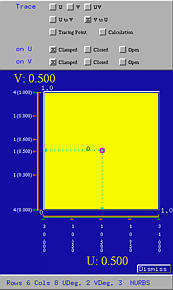
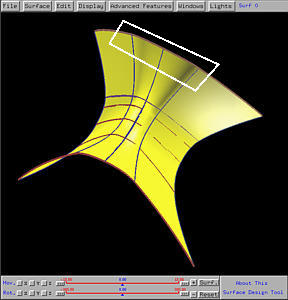
Changing the value of knot will change the shape of the surface. Dragging the little triangle of a knot will change its value. As a little triangle moves, its corresponding knot value changes accordingly. The following figures show the result of moving the knots 0.25 and 0.75 in the u-direction to 0.4 and 0.6, respectively, and knots 0.3, 0.5, 0.6 and 0.8 in the v-direction to 0.1, 0.2, 0.3 and 0.4, respectively. The change on the surface is not very clear; but, you can see some part of the surface becoming flatter (e.g., the part marked by the white rectangle).
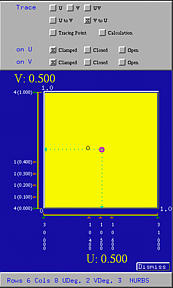
If a knot is moved on top of another, a multiple knot is created. Continue with the above example, if the knot 0.4 in the u-direction is moved to 0.5, making 0.5 a knot of multiplicity 2, and the knots 0.2 and 0.3 in the v-direction are moved to 0.1 and 0.5, respectively, making them multiple knots of multiplicity 2, we will have the following figure. You will see straight edges and the surface seems locally flat.
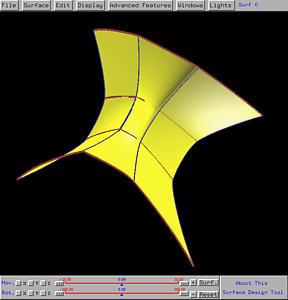
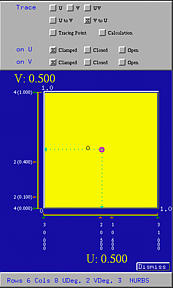
As a rule of thumb, changing knot values does not always yield satisfactory surface shape. In fact, it is hard to predict the change of surface shape as the result of changing the values of knots.