Ruled Surfaces

Given two curves C₁(u) and C₂(v), the ruled surface is the surface generated by connecting line segments between corresponding points, one on each given curve. More precisely, if t is a value in the domain [0,1] of both curves, a segment between C₁(t) and C₂(t) is constructed. This segment is usually referred as a ruling at t. As t moves from 0 to 1, the ruling at t sweeps out a surface and this is the ruled surface defined by curves C₁(u) and C₂(v).

To design a ruled surface, select Advanced Features followed by Cross Sectional Design. This will bring up the curve system. In the curve system, just design two NURBS curves that are not coplanar, and then select Techniques followed by Generate Ruled Surface. The surface system will display a ruled surface defined by the two curve in the curve system.

Note that these two curves do not have to be of the same degree with the same number of control points and the same number of knots. Note also that before sending the created surface to the surface system, the curve system will modify the two curves. As a result, the number of control points and the number of knots, and their positions shown in the surface system, in general, will not be the same as those in your original design.

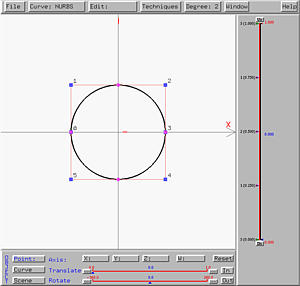
Many commonly seen and useful surfaces are ruled surfaces. Here are a few examples. Since circles will be frequently used, in case you forgot how to design a circle, click here to download a file (circle7.dat) in which a circle is defined as a NURBS curve of degree 2 using seven control points:

Example 1: Hyperbolic Paraboloid

The well-known saddle surface (i.e., hyperbolic paraboloid) is generated by two segments as a ruled surface. The following is the two line segments in the curve system, each of which is defined as a NURBS curve of degree 3 with four control points. As long as the control points are collinear, the curve is a line segment. Click here to download a copy of this file hp.dat.

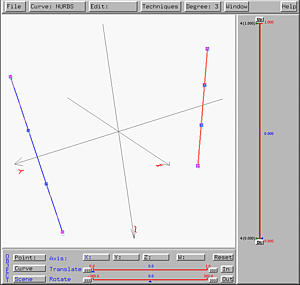
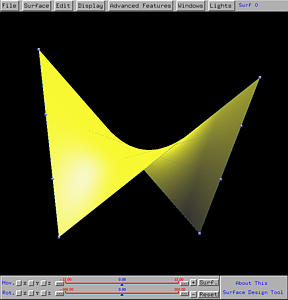
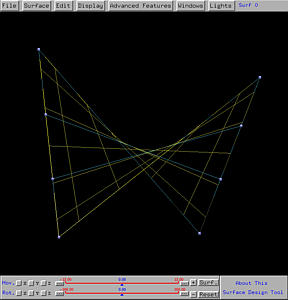
After sending this design to the surface system, we shall see the following hyperbolic paraboloid on the drawing canvas. The right figure shows clearly a few rulings.

Example 2: Cylinder

Cylinder is another well-known ruled surface. It is generated from two circles. In the curve system, one can create a circle in the xy-plane and save it. Then, import this circle back into the scene. This will produce two circles with the same orientation. Translating one of them in the z-direction would produce the desired circles. Click here to download a copy of this file cylinder.dat.

After sending this design to the surface system, we shall see the following cylinder on the drawing canvas. The right figure shows clearly a few rulings.

Example 3: Hyperboloid of One Sheet

A variation of the cylinder yields a hyperboloid of one sheet. What we need to do is rotating one of the two circles about the z-axis some degree. Click here to download a copy of this file hy.dat.

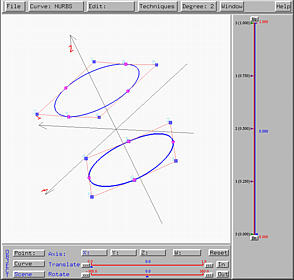
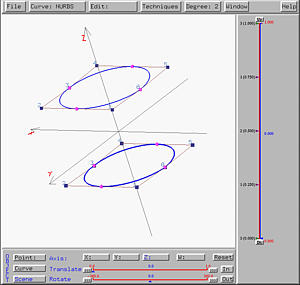
After sending this design to the surface system, we shall see the following hyperboloid of one sheet on the drawing canvas. The right figure shows clearly a few rulings between the two given circles.

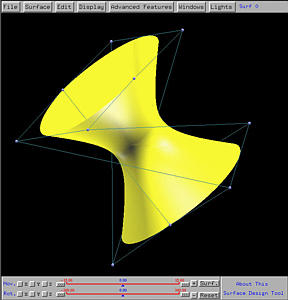
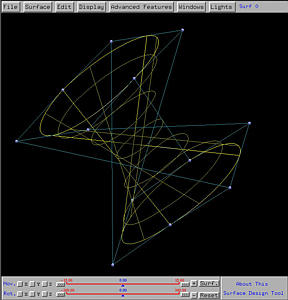
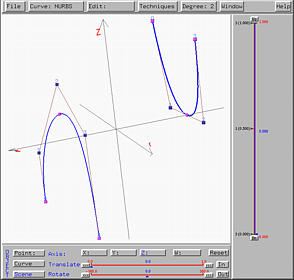
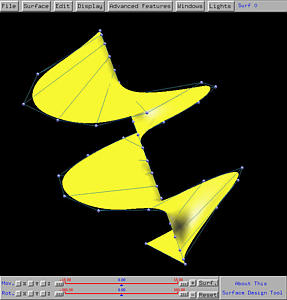
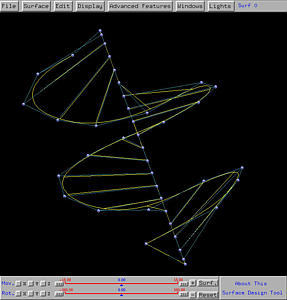
Example 4: A Ruled Surface Generated from Two Curves

The following are two NURBS curves. The one in the foreground is of degree 2 defined by five control points, and the one in the background is of degree 2 defined by four control points. Click here to download a copy of this file other.dat.

After sending this design to the surface system, we shall see the following ruled surface on the drawing canvas. The right figure shows clearly a few rulings between these two curves.

Example 5: An Interesting Surface

Let us design a helix-like surface. In the curve system, we first put a line segment in the z-axis as a degree 3 NURBS curve defined by four control points. Then, we put 21 control points in a spiral-like curve surrounding the z-axis. This is a NURBS curve of degree 3. These two curves are shown below. Click here to download a copy of this file helix.dat.

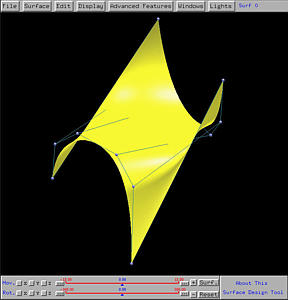
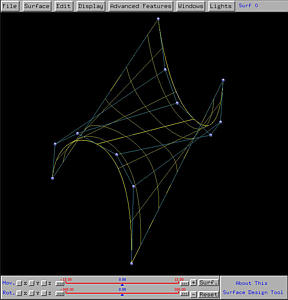
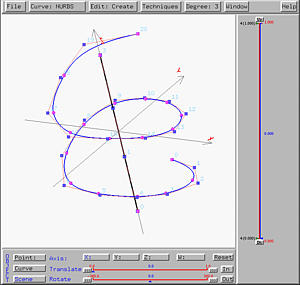
After sending this design to the surface system, we shall see the following ruled surface on the drawing canvas. The right figure shows clearly a few rulings between these two curves.