A Quick Tour

After launching the surface program you should see the following two windows:

The left one is the drawing canvas which is currently showing a default surface with a black background, while the right one is called the Tracing Window for you to control and trace the displayed surface.

Exiting the Program

To exit this program, choose File followed by Exit.

Showing the Control Net

Since a surface is given on the drawing canvas, we can use it to perform some display options. Under the Display button, there are several options:
  1. Selecting Show Control Net will cause the control net displayed as follows:

  2. To show control points, use Show Control Points. The result is the following:

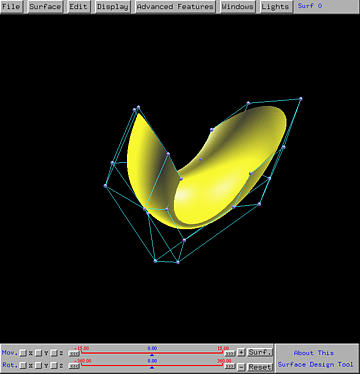
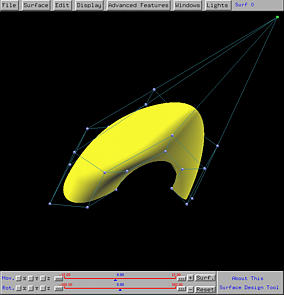
    All control points are shown as little white spheres.

  3. Each control point is assigned a row number and a column number. For example, 2,4 means the control point on row 2 and column 4. Please keep in mind that row and column numbers start with 0. To see these control point numbers, use Show Control Point IDs

  4. If you prefer to see the coordinate axes, use Show Axes. The x-, y- and z- axes will be displayed.

  5. By default, a parallel projection viewing system is used for displaying the surface. However, you can use Switch to Perspective Projection for a perspective view. The surface in general looks bigger. Control points closer to the viewing position look larger, while control points farther away look smaller. This is shown with the following figure.

    After perspective projection is activated, the menu option becomes Switch to Parallel Projection for you to switch back to parallel projection.

Note that all display options under Display will either show Show ... or Hide .... After an option is activated, the opposite will be shown in the menu.

Moving on the Surface

The Tracing Window provides important information about the surface being displayed and a way of tracing the surface. The bottom part shows the characteristics of the surface. Here, we see that the surface has 5 rows and 5 columns of control points, the degrees in both the u-direction and the v-directions are 3.

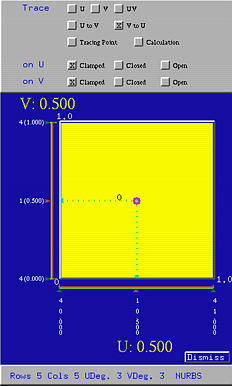
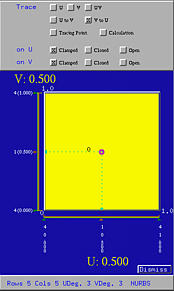
The big square in the middle is the unit square domain of the surface being displayed (i.e., [0,1]×[0,1]), where the u-direction is horizontal and the v-direction is vertical. Numbers below and to the left of the domain are knots. They are always in pairs with the first the multiplicity and the second the knot value.

There is a circular dot, the uv-indicator, with two dashed line segments giving its u value and v value. This is a point (u,v) that can be dragged in the unit square. As this indicator moves, the corresponding u and v values, which are shown in yellow, also change. To see the corresponding point on the surface, click on the Tracing Point button on the top part of this window. Then, the corresponding points on the surface is shown as a red sphere. The following shows the tracing point on the surface corresponding to (0.9, 0.53):

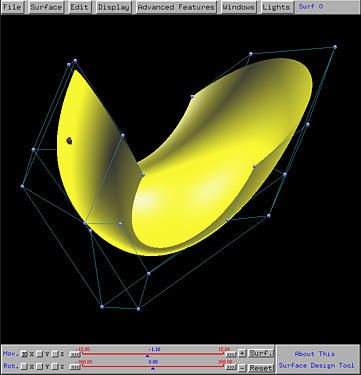
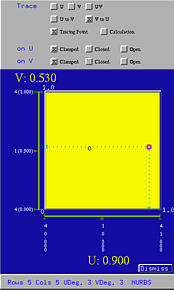
To deactivate this display option, click on the Tracing Point button again.

De Casteljau's and de Boor's Algorithms

Depending on the type of the surface being displayed, this system can display all intermediate polylines generated by the computation of de Casteljau's or de Boor's algorithm. To activate this capability, click on the Calculation button next to Tracing Point in the Tracing Window. In general, all polylines generated in one direction are shown in red while the last polyline in the other direction is shown in blue. The following is an example:

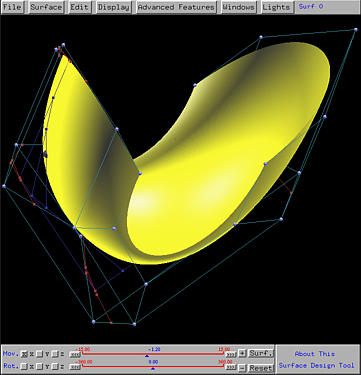
As the uv-indicator in the Tracing Window moves, the red sphere on the surface as well as all intermediate polylines move accordingly.

To deactivate this display option, click on the Calculation button again.

Changing the Positions of Control Points

Changing the position of a control point is easy, even though a surface has already been displayed. First, we should select a control point using the right mouse button. Then, a Control Point Update Window appears. It consists of four parts. The fourth (bottom) part is for modifying the weight of the selected control point, while the first three are small windows with grids for changing the coordinate values of the selected point.

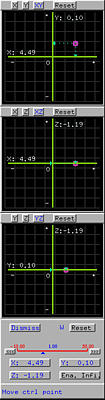
Dragging the little disk in the top window will cause the selected control point moving in the xy direction. More precisely, as the little disk moves, the x- and y-coordinate values of the selected control point will change and the z-coordinate is kept the same. Similarly, the second and the third windows are for moving a selected control point in the xz and yz directions, respectively. The x-, y- and z-coordinate and the weight w (if the surface is a NURBS surface) are displayed in the bottom of this window.

When the mouse pointer is in this window, clicking the right button pops up a menu with two items Large Steps and Small Steps. The former allows you to move the selected control point in a larger step size and the latter allows to use smaller step size.

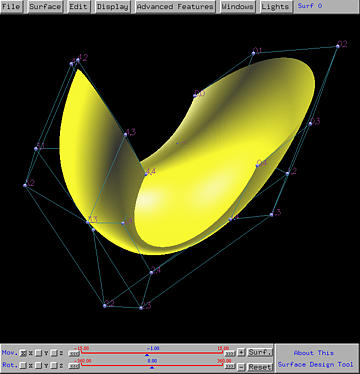
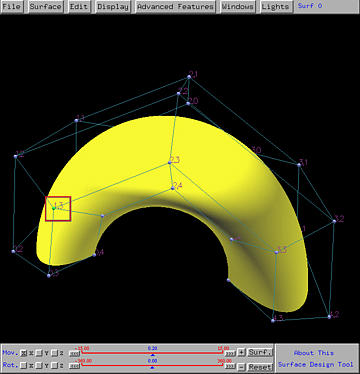
The following left figure shows a selected control point. After moving in the xy direction to a new position, the shape of the surface is changed (the right figure). In fact, part of the surface is pulled in the moving direction of the selected control point.

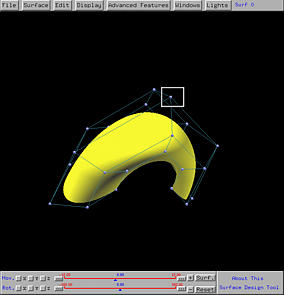
The Reset buttons on the top of each small window reset the control point back to the position before this move, and the Dismiss button closes this window. Note that resetting may not be very accurate due to the fact that some mouse activities may not be caught precisely.

For the Sake of Displaying Speed

Since rendering a surface is time consuming, this system provides four levels of details for wireframe rendering. Under Display, option Rendering Method is designed for this purpose. It has two options, namely Patch and Wireframe. The former produces a shaded surface and the latter only draws lines. There are four different levels of details, the higher the more detail. The following shows a detail level 4 wireframe of the surface seen in all previous figures.

Moving the Surface Around

This system supports two types of transformations, transforming the surface and transforming the scene. The bottom part of the drawing canvas is designed for performing transformations. It has two horizontal sliders, the top one for translation while the bottom one for rotation, where X, Yand Z are buttons indicating the reference coordinate axis. The right end has four more buttons: + and - are for zooming in and out, respectively, and Surf. and Scene indicate the transformation is applied to the displayed surface and to the whole scene, respectively. Finally, Reset will restore the surface or the scene back to its initial position.

To perform a translation or a rotation to the scene or to the surface, you must select the object to be transformed and a reference coordinate axis. For example, to translate the scene in the y-direction, one must click on the Surf. button to make Scene to appear. However, if Scene is shown, the transformation will be applied to the scene. Then, select Y and drag the Move slider. This will cause the whole scene moved in the y direction. You can also click on button >>> (resp., <<<) to increase (resp., decrease) the amount of translation and rotation.

To zoom in (i.e., moving the camera closer to the surface), use button +; and to zoom out (i.e., moving the camera farther way from the surface), use button -.

This system supports a second way of performing translations and rotations to the scene. Here is how.

  1. The left mouse button is for rotation. The surface rotates in the direction of the mouse movement.
  2. The middle mouse button is for translation. The surface translates in the direction of the mouse movement.

If your machine is not fast enough, some mouse movements would not be caught on time and some many even lost. As a result, the sliders may not be able to provide accurate movements. If this happens, use wireframe display method.

In many cases, having the coordinate axes shown will help to position the surface or the scene to a desired place. You can select Display followed by Show Axes to display the coordinate axes or Hide Axes to hide the coordinate axes.

Partition of Unity

Since basis functions play an important role in generating a surface, this system can display these basis functions and partition of unity. To do so, choose Window followed by Show Partition of Unity Window. The Partition of Unity window appears. If a control point is selected by clicking on it with the right mouse button, the coefficient of that control point will be shown as a wireframe surface. Note that the coefficient of a control point is a function of two variables u and v and is the product of two one-dimensional basis functions. This window will also show these two one-dimensional basis functions. Since the sum of all basis functions in one direction is 1, this window shows two line segments whose subdivisions, shown in different colors, form the partition of unity in that direction. Dragging the uv-indicator will cause the partitions of unity to change.

To close this window, select the Dismiss button at the lower left corner of this window.

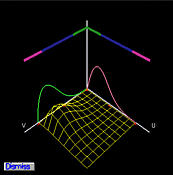
The above left figure shows a B-spline surface with control point 1,3 (i.e., row 1 and column 3) selected. Thus, the Partition of Unity window shows N1,p(u) in the u direction and N3,q(v) in the v direction. Note that p and q are the degrees in the u and v directions. The product, N1,p(u)N3,q(v), is the coefficient (i.e., two-dimensional basis function) for control point 1,3.

Implicit Surfaces

This system has incorporated Jules Bloomenthal's polygonizer for displaying implicit surfaces. This polygonizer only works well with C1 surfaces; otherwise, the results may be incomplete, have truncated edges, or contain small jutting pieces.

To use this polygonizer, click on Surface followed by Implicit Surface. This will load the polygonizer into this system. Before you can display a surface, an implicit equation must be given. If you choose Define Implicit Surface, your will see a window for you to type in your equation that defines the surface. In fact, you type in the equation through a text editor running in the newly opened window. You can also select Define Your Editor to choose your favorable editor. Note that this editor must be accessible via the current path.

What you have to do are (1) declaring variables you want to use in the function myfunc() and (2) returning the result of evaluating your implicit equation with variable rsq. For example, the torus in a "standard" position has the following implicit equation:

(x2 + y2 + z2 - ( R2 - r2))2 - 4R2(r2 - z2) = 0

Function myfunc() should be 

double myfunc (double x, double y, double z)
{
    double rsq;  /* return value    */
    double R = 2.0, r = 1.0, temp;

    temp = x*x + y*y + z*z - (R*R + r*r);
    rsq  = temp*temp - 4.0*R*R*(r*r - z*z);
    return rsq;  /* must return this value */
}
Then, save your equation, wait for a while and the drawing canvas will display a torus:

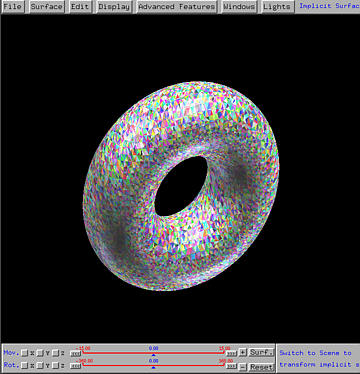
The polygonizer subdivides the surface of the torus into 31068 triangles with 15534 vertices. Each triangle is displayed with a random color as shown in the above figure.

When this implicit surface feature activated (i.e., an implicit surface is shown on the drawing canvas), You can only translate and rotate the scene, and you must use the sliders for translations and rotations, and + and - for zooming.

To switch back to parametric surfaces, select Surface, followed by Unload Implicit Surface.