Shape Modification - Modifying Weights

To modify the shape of a surface, one can change the position of control points, and remove a row or a column of control points. If the surface is a rational Bézier or a NURBS surface, one can change the weight of a control point. If the surface is a B-spline or a NURBS, one can also change the positions of knots. Note that one cannot add control points; but, one can add knots by knot insertion without changing the shape of the surface. This page focuses on modifying weights.

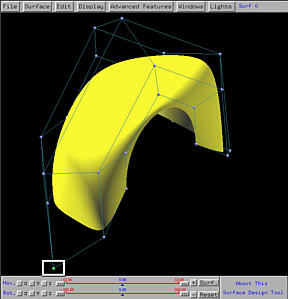
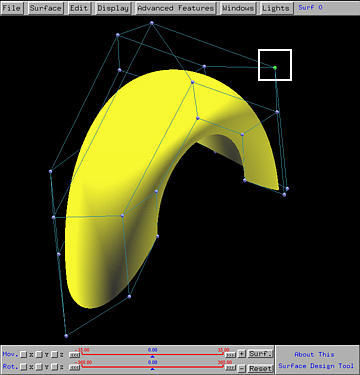
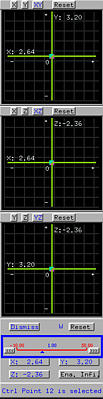
Note that only the control points of a rational Bézier and a NURBS surface can have weight. The weights of control points of a Bézier and a B-spline surface are all 1s and are fixed (i.e., cannot be changed). Let us load the default scene one, which is a NURBS surface, and select the control point marked with the white rectangle using the right mouse button. The Control Point Update Window appears. The bottom part of this window shows the coordinates of this control point. The little slider, marked with a blue rectangle below, gives the current weight associated with the selected control point. Sliding the little triangle will change the value of weight.

The general rule of changing weight is

• Increasing the weight of a control point pulls the surface toward that control point. If the weight value of the selected control point is increased to 2, the surface is slightly pulled toward that control point (the left figure below). If the weight value is further increased to 5, it is clear that the surface is pulled further and closer to the control point. In fact, if the weight is increased to infinity, the surface will pulled to pass through the control point!
  

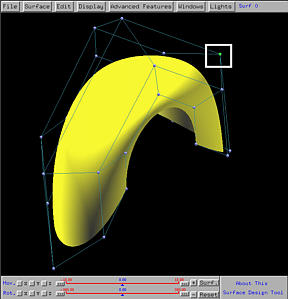
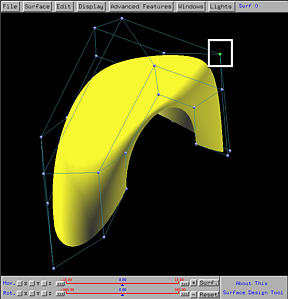
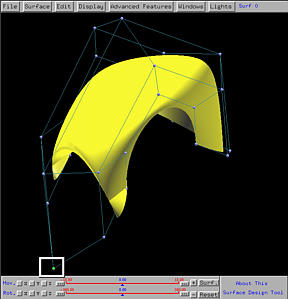
  If you compare all three figures, increasing the weight of a control point only affects the area it has influence, while keeps the other parts of the surface unchanged. This is a direct consequence of the local modification property, which means that the impact of a modification on a control point, its weight, or a knot, is local.

• Decreasing the weight of a control point pushes the surface away from that control point. The left figure below shows the result decreasing the weight of the selected control point from 1 to 0.5. Comparing with the corresponding figure above, one can see that the surface is flatter near that control point. If the weight is decreased to 0.1 (the right figure below), the surface becomes even flatter.
  

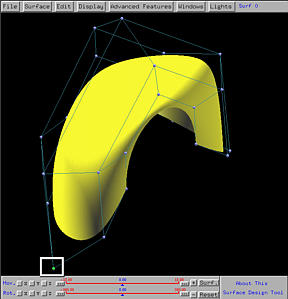
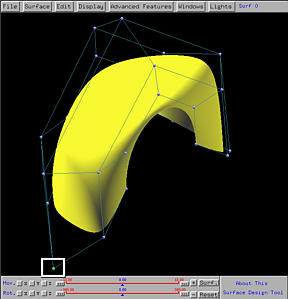
  In practice, the weight of a control point should be non-negative. If the weight of a control point is decreased to zero, this means that control point has no influence to the surface and as a result the region near that control point should be flat (the left figure below). If the weight is changed to a negative value, the surface will be pushed further and unpleasant effect may occur. In the right figure below, the weight is changed to -0.6, the surface looks bent and part of it lies outside of the convex hull of the control points. This violates the convex hull property. Thus, in general, do not use negative weights .