Solving Systems of Linear Equations

Since solving a system of linear equations is a basic skill that will be used for interpolation and approximation, we will briefly discuss a commonly used technique here. In fact, what we will be using is a slightly more general form. Suppose we have a n×n coefficient matrix A, a n×h "constant" term matrix B, and a n×h unknown matrix X defined as follows:

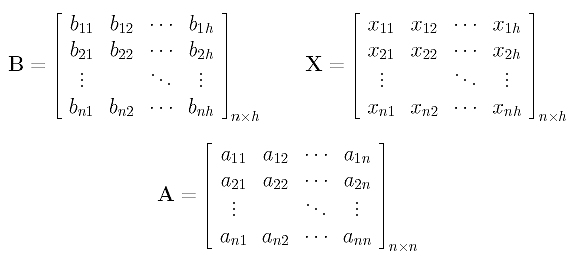
Suppose further that they satisfy the following relation:

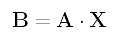
If A and B are known, we need a fast method to solve for X. One may suggest the following: compute the inverse matrix A^-1 of A and the solution is simply X = A^-1B. While this is a correct way to solve the problem, it is a little overkill. One might also observe the following fact: column j of matrix B is the product of matrix A and column j of matrix X as shown below:

With this in mind, we can solve column j of X using A and column j of B. In this way, the given problem is equivalent to solving h systems of linear equations. Actually, this is not a good strategy either because in solving for column 1 of X matrix A will be destroyed, and, as a result, for each column we need to make a copy of matrix A before running the linear system solver.

So, we need a method that does not use matrix inversion and does not have to copy matrix A over and over. A possible way is the use of the LU decomposition technique.

LU Decomposition

An efficient procedure for solving B = A^.X is the LU-decomposition. While other methods such as Gaussian elimination method and Cholesky method can do the job well, this LU-decomposition method can help accelerate the computation.

The LU-decomposition method first "decomposes" matrix A into A = L^.U, where L and U are lower triangular and upper triangular matrices, respectively. More precisely, if A is a n×n matrix, L and U are also n×n matrices with forms like the following:

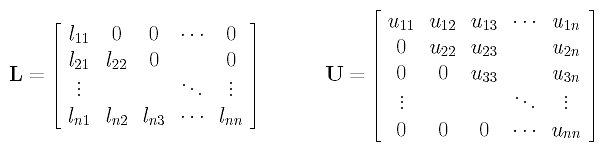
The lower triangular matrix L has zeros in all entries above its diagonal and the upper triangular matrix U has zeros in all entries below its diagonal. If the LU-decomposition of A = L^.U is found, the original equation becomes B = (L^.U)^.X. This equation can be rewritten as B = L^.(U^.X). Since L and B are known, solving for B = L^.Y gives Y = U^.X. Then, since U and Y are known, solving for X from Y = U^.X yields the desired result. In this way, the original problem of solving for X from B = A^.X is decomposed into two steps:

1. Solving for Y from B = L^.Y
2. Solving for X from Y = U^.X

Forward Substitution

How easy are these two steps? It turns out to be very easy. Consider the first step. Expanding B = L^.Y gives

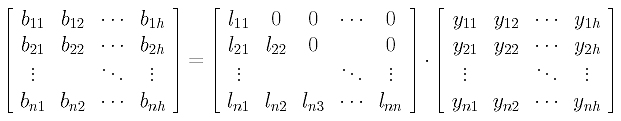
It is not difficult to verify that column j of matrix B is the product of matrix A and column j of matrix Y. Therefore, we can solve one column of Y at a time. This is shown below:

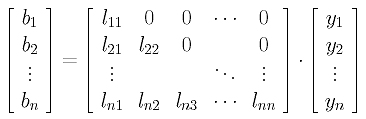
This equation is equivalent to the following:

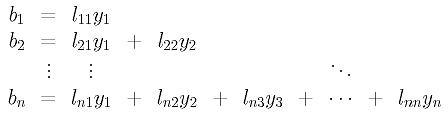
From the above equations, we see that y₁ = b₁/l₁₁. Once we have y₁ available, the second equation yields y₂ = (b₂-l₂₁y₁)/l₂₂. Now we have y₁ and y₂, from equation 3, we have y₃ = (b₃ - (l₃₁y₁ +l₃₂y₂)/l₃₃. Thus, we compute y₁ from the first equation and substitute it into the second to compute y₂. Once y₁ and y₂ are available, they are substituted into the third equation to solve for y₃. Repeating this process, when we reach equation i, we will have y₁, y₂, ..., y_i-1 available. Then, they are substituted into equation i to solve for y_i using the following formula:

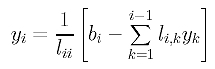
Because the values of the y_i's are substituted to solve for the next value of y, this process is referred to as forward substitution. We can repeat the forward substitution process for each column of Y and its corresponding column of B. The result is the solution Y. The following is an algorithm:

Input: Matrix B_n×h and a lower triangular matrix L_n×h
Output: Matrix Y_n×h such that B = L^.Y holds.
Algorithm:

/* there are h columns */
for j := 1 to h do
/* do the following for each column */
begin

/* compute y₁ of the current column */
y_1,j = b_1,j / l_1,1;
for i := 2 to n do /* process elements on that column */
begin

sum := 0; /* solving for y_i of the current column */
for k := 1 to i-1 do

sum := sum + l_i,k× y_k,j;

y_i,j = (b_i,j - sum)/l_i,i;
end
end

Backward Substitution

After Y becomes available, we can solve for X from Y = U^.X. Expanding this equation and only considering a particular column of Y and the corresponding column of X yields the following:

This equation is equivalent to the following:

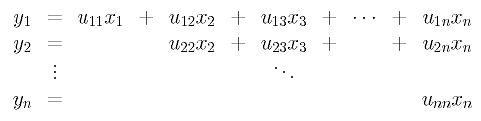
Now, x_n is immediately available from equation n, because x_n = y_n/u_n,n. Once x_n is available, plugging it into equation n-1

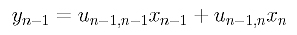
and solving for x_n-1 yields x_n-1 = (y_n-1- u_n-1,nx_n)/ u_n-1,n-1. Now, we have x_n and x_n-1. Plugging them into equation n-2

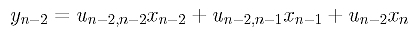
and solving for x_n-2 yields x_n-2 = [y_n-2- (u_n-2,n-1x_n-1 + u_n-2,nx_n-)]/ u_n-2,n-2.

From x_n, x_n-1 and x_n-2, we can solve for x_n-3 from equation n-3. In general, after x_n, x_n-1, ..., x_i+1 become available, we can solve for x_i from equation i using the following relation:

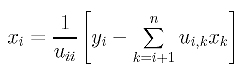
Repeat this process until x₁ is computed. Then, all unknown x's are available and the system of linear equations is solved. The following algorithm summarizes this process:

Input: Matrix Y_n×h and a upper triangular matrix U_n×h
Output: Matrix X_n×h such that Y = U^.X holds.
Algorithm:

/* there are h columns */
for j := 1 to h do
/* do the following for each column */
begin

/* compute x_n of the current column */
x_n,j = y_n,j / u_n,n;
for i := n-1 downto 1 do /* process elements of that column */
begin

sum := 0; /* solving for x_i on the current column */
for k := i+1 to n do

sum := sum + u_i,k× x_k,j;

x_i,j = (y_i,j - sum)/u_i,i;
end
end

This time we work backward, from x_n backward to x₁, and, hence, this process is referred to as backward substitution.

LU-decomposition and forward and backward substitutions, including their subroutines/functions, should be available in many numerical method textbooks and mathematical libraries. Check your numerical methods textbook for the details.