Parametric Curves: A Review

As mentioned in the discussion of boundary representations, each face is surrounded by edges, which could be line segments or curve segments, and the face itself is part of a surface (i.e., a surface patch). In this unit, we shall discuss the general concept of curve segments in parametric form.

A parametric curve in space has the following form:

f: [0,1] -> ( f(u), g(u), h(u) )

where f(), g() and h() are three real-valued functions. Thus, f(u) maps a real value u in the closed interval [0,1] to a point in space. The domain of these real functions and vector-valued function f() does not have to be [0,1]. It can be any closed interval; but, for simplicity, we restrict the domain to [0,1]. Thus, for each u in [0,1], there corresponds to a point ( f(u), g(u), h(u) ) in space.

In this course, functions f(), g() and h() are always polynomials.

Note that if function h() is removed from the definition of f(), f() has two coordinate components and becomes a curve in the coordinate plane.

Examples

We have seen that a straight line is defined as B+td, where B is a base point and d is a direction vector. Thus, if f() is defined as
f(u) = b₁ + ud₁
g(u) = b₂ + ud₂
h(u) = b₃ + ud₃

where B = < b₁, b₂, b₃ >, d = < d₁, d₂, d₃ >, and f() is a parametric curve that maps [0,1] to the line segment between B and B+d, inclusive.
A circle has the following non-polynomial form:
x(u) = rcos(2*PI*u) + p
y(u) = rsin(2*PI*u) + q

It has center (p, q) and radius r. Since the parameter u is in [0,1], the value of 2*PI*u is in [0,2*PI] (i.e., from 0 degree to 360 degree).
Let us eliminate u. First, change the above equations to the following. For convenience, we drop (u) from x(u) and y(u).
x - p = rcos(2*PI*u)
y - q = rsin(2*PI*u)

Then, squaring both equations and adding them together yields
(x - p)² + (y - q)² = r²
Thus, it shows that the given parametric curve is indeed a circle with center at (p, q) and radius r.
A space cubic curve has the following form:
f(u) = u
g(u) = u²
h(u) = u³
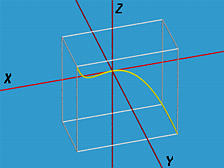
The following figure shows this curve in the range of [-1,1]. It is contained in the box (in white) defined by ( -1, 0, -1 ) and (1, 1, 1)
The circular helix is defined as follows:
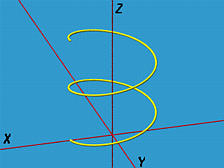
f(u) = ( acos(u), asin(u), bu )
The following figure shows the curve in [0, 4*PI]. The initial point is (a, 0, 0) and the endpoint is (a, 0, b*4*PI). Note that this curve lies on the cylinder of radius a and axis the z-axis.