Normal Vector and Curvature

Consider a fixed point f(u) and two moving points P and Q on a parametric curve. These three points determine a plane. As P and Q moves toward f(u), this plane approaches a limiting position. This is the osculating plane at f(u). Obviously, the osculating plane at f(u) contains the tangent line at f(u). It can be shown that the osculating plane is the plane that passes through f(u) and contains both f'(u) and f''(u). More precisely, any point on this plane has an equation as follows, where p and q are parameters:

f(u) + pf'(u) + qf''(u)

The binormal vector b(u) is the unit-length vector of the cross-product of f'(u) and f''(u):

b(u) = (f'(u) × f''(u)) / | (f'(u) × f''(u)) |

Thus, the binormal vector b(u) is perpendicular to both f'(u) and f''(u) and hence perpendicular to the osculating plane. The line f(u)+tb(u) is the binormal line at f(u).

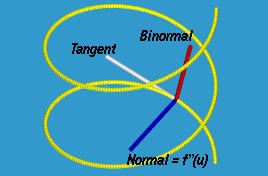
The normal vector is the vector perpendicular to both tangent and binormal vectors with its direction determined by the right-handed system. That is, the unit-length normal vector n(u) is defined to be

n(u) = ( b(u) × f'(u) ) / | b(u) × f'(u) |

The line f(u)+tn(u) is the normal line at f(u). Therefore, tangent vector f'(u), normal vector n(u) and binormal vector b(u) form a coordinate system with origin f(u). The tangent line, binormal line and normal line are the three coordinate axes with positive directions given by the tangent vector, binormal vector and normal vector, respectively. These three vectors are usually referred to as the moving triad or triad at point f(u). Moving triad is also called moving trihedron. The following figure shows their relationship. Note that the tangent, normal and f''(u) vectors are on the same plane.

An Example

Let us compute the tangent, binormal and normal vectors of the circular helix curve:

f(u) = ( acos(u), asin(u), bu )

The first and second derivatives are as follows:

f'(u) = ( -asin(u), acos(u), b )
f''(u) = ( -acos(u), -asin(u), 0 )

The non-unit-length binormal vector is the cross-product of f'(u) and f''(u), in this order:

b(u) = f'(u) × f''(u) = ( absin(u), -abcos(u), a² )

The non-unit-length normal vector is the cross-product of the binormal vector and the tangent vector, in this order:

n(u) = b(u) × f'(u) = ( -a(a² + b²)cos(u), -a(a² + b²)sin(u), 0 )

If you compare n(u) and f''(u), you will see that these vectors are parallel to each other (i.e., coefficients are proportional) and are both parallel to the xy-plane. As a result, after normalizing all involving vectors, the normal and the second derivative vectors are identical. This is shown by the following figure. It is computed at u = 1.

Curvature

As we all know, the tangent vector measures the change of "distance" and thus gives the speed of a moving point. The speed change, or acceleration, is measured by the derivative of the tangent vector, which is the second derivative. In fact, there is one more interesting interpretation. Take X as a fixed point and P and Q two moving points. As long as not all of these three points lie on a line, they uniquely determine a circle. As both P and Q moves toward X, the circle they determine approaches a limiting position as shown with dot-line below. This limiting circle is called the circle of curvature at X and its center and radius, O and r, are the center and radius of circle of curvature, respectively. More importantly, 1/r is the curvature at X. Therefore, the larger the circle of curvature, the smaller the curvature.

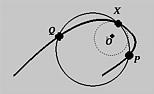
From the definition of osculating plane, we know that this circle of curvature must be on the osculating plane. Since the circle of curvature is tangent to the curve and hence the tangent line, the center of curvature lies on the normal line.

The curvature at u, k(u), can be computed as follows:

k(u) = | f'(u) × f''(u) | / | f'(u) |³

Let us continue with the previous example of the circular helix curve. From the computations of f'(u) and f''(u), we have

f'(u) = ( -asin(u), acos(u), b )
f'(u) × f''(u) = ( absin(u), -abcos(u), a² )
| f'(u) | = SQRT(a² + b²)
| f'(u) × f''(u) | = aSQRT(a² + b²)
k(u) = a / (a² + b²)

Therefore, the curvature at any point on the curve is a constant a/(a² + b²).

Since the radius of the circle of curvature is 1/k, we see that the center of circle of curvature is located at a distance of (a² + b²)/a from f(u) in the normal direction n(u).

More Examples

Consider a straight line:
f(u) = ( a + up, b + uq, c + ur )
We have the following:
f'(u) = ( p, q, r )
| f'(u) | = SQRT(p² + q² + r²)
f''(u) = ( 0, 0, 0 )
f'(u) × f''(u) = ( 0, 0, 0 )
k(u) = 0
Therefore, the curvature of a straight line is zero everywhere. Note that none of the binormal and normal vectors is well-defined because f''(u) is a zero vector.
Consider a circle on the xy-plane:
f(u) = ( rcos(u) + p, rsin(u) + q, 0 )
Since it is on the xy-plane, the third coordinate function is always 0. From the given circle's equation we have the following:
f'(u) = ( -rsin(u), rcos(u), 0 )
f''(u) = ( -rcos(u), -rsin(u), 0 )
f'(u) × f''(u) = ( 0, 0, r² )
| f'(u) | = r
| f'(u) × f''(u) | = r²
b(u) = (f'(u) × f''(u)) / | f'(u) × f''(u) | = ( 0, 0, 1 )
n(u) = (b(u) × f'(u)) / | b(u) × f'(u) | = ( -cos(u), -sin(u), 0 )
k(u) = 1/r
Thus, the unit-length tangent vector is (-sin(u), cos(u), 0), the binormal vector is ( 0, 0, 1), and the normal vector is ( -cos(u), sin(u), 0). The binormal vector is always perpendicular to the xy-plane while both the tangent and normal vectors lie on the xy-plane. The curvature of a circle is a constant 1/r. As a result, the radius of the circle of curvature is r and the circle of curvature is the given circle itself.
Consider the space cubic defines as follows:
f(u) = ( u, u², u³ )
The following are the computation of curvature k(u):
f'(u) = ( 1, 2u, 3u² )
| f'(u) | = SQRT(1 + 4u² + 9u⁴ )
f''(u) = ( 0, 2, 6u)
f'(u) × f''(u) = ( 6u², -6u, 2 )
| f'(u) × f''(u) | = 2SQRT(1 + 9u² + 9u⁴)
k(u) = 2SQRT(1 + 9u² + 9u⁴) / (SQRT(1 + 4u² + 9u⁴ ))³

Why Is the Moving Triad Important?

The moving triad is not only a mathematical concept. It also provides vital information of the characteristics of a moving object. For example, if you are on a airplane or a roller-coaster, as you are "flying" you are following a curve. Therefore, you are moving in the direction of the tangent vector, your "up" vector is in the direction of the binormal vector and the rate of turning and turning direction are given by the curvature and the direction of the normal vector, respectively. That is, while you are rolling or tumbling, this triad always provides you with the forward, up and turning directions. Therefore, to correctly animate a moving object, you need to know the geometric characteristics of the moving triad.

There is one more parameter, the torsion, that describing the way of twisting of a space curve. A planar curve does not twist and hence its torsion is zero. Since we will not use torsion in this course, it will not be introduced here. See your calculus or differential geometry books for the details.