Tangent Vector and Tangent Line

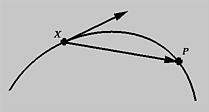
Consider a fixed point X and a moving point P on a curve. As point P moves toward X, the vector from X to P approaches the tangent vector at X. The line that contains the tangent vector is the tangent line.

Computing the tangent vector at a point is very simple. Recall from your calculus knowledge that the derivative of parametric curve f(u) is the following:

f'(u) = ( f'(u), g'(u), h'(u) )

In general, the length of the tangent vector f'(u) is not one, and normalization is required. That is, the unit-length tangent vector at parameter u, or at point f(u), is

f'(u) / | f'(u) |

f(u) + tf'(u)

f(u) + t(f'(u)/|f'(u)|)

Examples

• Consider the circle f(u) = ( rcos(2*PI*u) + p, rsin(2*PI*u) + q ), where u is in the range of 0 and 1. We have the tangent vector at u as follows:

  f'(u) = ( -2*PI*rsin(2*PI*u), 2*PI*rcos(2*PI*u) )

  and the tangent line at f(u):

  f(u) + tf'(u) = ( rcos(2*PI*u) + p, rsin(2*PI*u) + q ) + t ( -2*PI*rsin(2*PI*u), 2*PI*rcos(2*PI*u)

• Consider a space cubic curve f(u) = ( u, u², u³ ). We have tangent vector f'(u) = ( 1, 2u, 3u² ) and tangent line f(u) + tf'(u) = ( u + t, u² + 2tu, u³ + 3tu² ), where t is the line parameter.
• The circular helix curve has an equation as follows:

  f(u) = ( acos(u), asin(u), bu )

  It has tangent vector

  f'(u) = ( -asin(u), acos(u), b )

  and tangent line

  f(u) + tf'(u) = ( a(cos(u) - tsin(u)), a(sin(u) + tcos(u)), b(t+u) )