Geometric Transformations

When talking about geometric transformations, we have to be very careful about the object being transformed. We have two alternatives, either the geometric objects are transformed or the coordinate system is transformed. These two are very closely related; but, the formulae that carry out the job are different. We only cover transforming geometric objects here.

We shall start with the traditional Euclidean transformations that do not change lengths and angle measures, followed by affine transformation. Finally, we shall talk about projective transformations.

Euclidean Transformations

The Euclidean transformations are the most commonly used transformations. An Euclidean transformation is either a translation, a rotation, or a reflection. We shall discuss translations and rotations only.

Translations and Rotations on the xy-Plane

We intend to translate a point in the xy-plane to a new place by adding a vector <h, k> . It is not difficult to see that between a point (x, y) and its new place (x', y'), we have x' = x + h and y' = y + k. Let us use a form similar to the homogeneous coordinates. That is, a point becomes a column vector whose third component is 1. Thus, point (x,y) becomes the following:

Then, the relationship between (x, y) and (x', y') can be put into a matrix form like the following:

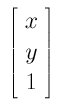
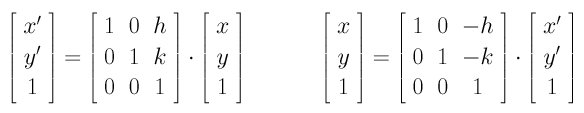
Therefore, if a line has an equation Ax + By + C = 0, after plugging the formulae for x and y, the line has a new equation Ax' + By' + (-Ah - Bk + C) = 0.

If a point (x, y) is rotated an angle a about the coordinate origin to become a new point (x', y'), the relationships can be described as follows:

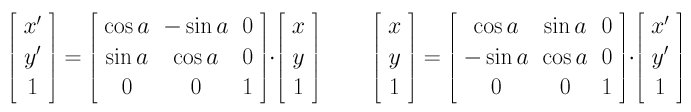
Thus, rotating a line Ax + By + C = 0 about the origin a degree brings it to a new equation:

(Acosa - Bsina)x' + (Asina + Bcosa)y' + C = 0

Translations and rotations can be combined into a single equation like the following:

The above means that rotates the point (x,y) an angle a about the coordinate origin and translates the rotated result in the direction of (h,k). However, if translation (h,k) is applied first followed by a rotation of angle a (about the coordinate origin), we will have the following:

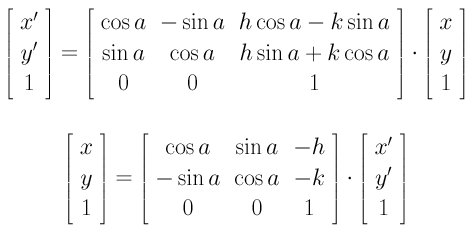
Therefore, rotation and translation are not commutative!

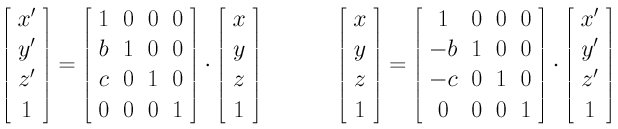
In the above discussion, we always present two matrices, A and B, one for transforming x to x' (i.e., x'=Ax) and the other for transforming x' to x (i.e., x=Bx'). You can verify that the product of A and B is the identity matrix. In other words, A and B are inverse matrices of each other. Therefore, if we know one of them, the other is the inverse of the given one. For example, if you know A that transforms x to x', the matrix that transforms x' back to x is the inverse of A.

Let R be a transformation matrix sending x' to x: x=Rx'. Plugging this equation of x into a conic equation gives the following:

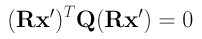
Rearranging terms yields

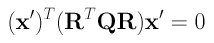
This is the new equation of the given conic after the specified transformation. Note that the new 3-by-3 symmetric matrix that represents the conic in a new position is the following:

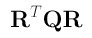
Now you see the power of matrices in describing the concept of transformation.

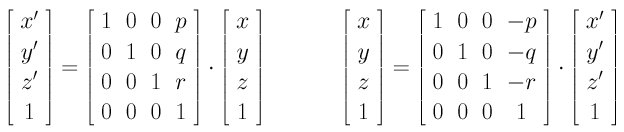
Translations and Rotations in Space

Translations in space is similar to the plane version:

The above translates points by adding a vector <p, q, r>.

Rotations in space are more complex, because we can either rotate about the x-axis, the y-axis or the z-axis. When rotating about the z-axis, only coordinates of x and y will change and the z-coordinate will be the same. In effect, it is exactly a rotation about the origin in the xy-plane. Therefore, the rotation equation is

With this set of equations, letting a be 90 degree rotates (1,0,0) to (0,1,0) and (0,1,0) to (-1,0,0). Therefore, the x-axis rotates to the y-axis and the y-axis rotates to the negative direction of the original x-axis. This is the effect of rotating about the z-axis 90 degree.

Based on the same idea, rotating about the x-axis an angle a is the following:

Let us verify the above again with a being 90 degree. This rotates (0,1,0) to (0,0,1) and (0,0,1) to (0,-1,0). Thus, the y-axis rotates to the z-axis and the z-axis rotates to the negative direction of the original y-axis.

But, rotating about the y-axis is different! It is because the way of measuring angles. In a right-handed system, if your right hand holds a coordinate axis with your thumb pointing in the positive direction, your other four fingers give the positive direction of angle measuring. More precisely, the positive direction for measuring angles is from the z-axis to x-axis. However, traditionally the angle measure is from the x-axis to the z-axis. As a result, rotating an angle a about the y-axis in the sense of a right-handed system is equivalent to rotating an angle -a measuring from the x-axis to the z-axis. Therefore, the rotation equations are

Let us verify the above with rotating about the y-axis 90 degree. This rotates (1,0,0) to (0,0,-1) and (0,0,1) to (1,0,0). Therefore, the x-axis rotates to the negative direction of the z-axis and the z-axis rotates to the original x-axis.

A rotation matrix and a translation matrix can be combined into a single matrix as follows, where the r's in the upper-left 3-by-3 matrix form a rotation and p, q and r form a translation vector. This matrix represents rotations followed by a translation.

You can apply this transformation to a plane and a quadric surface just as what we did for lines and conics earlier.

Affine Transformations

Euclidean transformations preserve length and angle measure. Moreover, the shape of a geometric object will not change. That is, lines transform to lines, planes transform to planes, circles transform to circles, and ellipsoids transform to ellipsoids. Only the position and orientation of the object will change. Affine transformations are generalizations of Euclidean transformations. Under affine transformations, lines transforms to lines; but, circles become ellipses. Length and angle are not preserved. In this section, we shall discuss scaling, shear and general affine transformations.

Scaling

Scaling transformations stretch or shrink a given object and, as a result, change lengths and angles. So, scaling is not an Euclidean transformation. The meaning of scaling is making the new scale of a coordinate direction p times larger. In other words, the x coordinate is "enlarged" p times. This requirement satisfies x' = p x and therefore x = x'/p.

Scaling can be applied to all axes, each with a different scaling factor. For example, if the x-, y- and z-axis are scaled with scaling factors p, q and r, respectively, the transformation matrix is:

Shear

The effect of a shear transformation looks like ``pushing'' a geometric object in a direction parallel to a coordinate plane (3D) or a coordinate axis (2D). In the following, the red cylinder is the result of applying a shear transformation to the yellow cylinder:

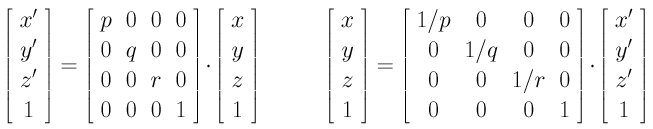
How far a direction is pushed is determined by a shearing factor. On the xy-plane, one can push in the x-direction, positive or negative, and keep the y-direction unchanged. Or, one can push in the y-direction and keep the x-direction fixed. The following is a shear transformation in the x-direction with shearing factor a:

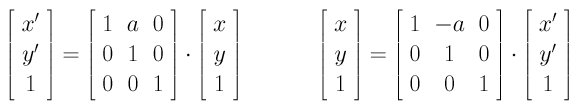
The shear transformation in the y-direction with shearing factor b is the following:

In space, one can push in two coordinate axis directions and keep the third one fixed. The following is the shear transformation in both x- and y-directions with shearing factors a and b, respectively, keeping the z-coordinate the same:

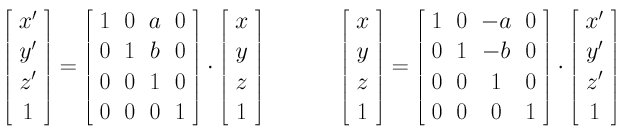
Let us take a look at the effect of this shear transformation. Expanding the matrix equation gives the following:

x' = x + az
y' = y + bz
z' = z

Thus, a point (x, y, z) in space is transformed to (x + az, y + bz, z). Therefore, the z-coordinate does not change, while (x, y) is ``pushed'' in the direction of (a, b, 0) with a factor z.

The following is the shear transformation in xz-direction:

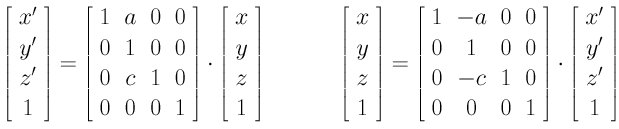
The following is the shear transformation in yz-direction:

General Affine Transformations

The general affine transformation matrix has the following form:

Comparing with all previous discussed matrices, rotations and translations included, you will see that all of them fit into this form and hence are affine transformations. Affine transformations do not alter the degree of a polynomial, parallel lines/planes are transformed to parallel lines/planes, and intersecting lines/plane are transformed to intersecting lines and planes. However, affine transformations do not preserve lengths and angle measures and as a result they will change the shape of a geometric object. The following shows the result of a affine transformation applied to a torus. A torus is described by a degree four polynomial. The red surface is still of degree four; but, its shape is changed by an affine transformation.

Note that the matrix form of an affine transformation is a 4-by-4 matrix with the fourth row 0, 0, 0 and 1. Moreover, if the inverse of an affine transformation exists, this affine transformation is referred to as non-singular; otherwise, it is singular. We do not use singular affine transformations in this course.

Projective Transformations

Projective transformations are the most general "linear" transformations and require the use of homogeneous coordinates. Given a point in space in homogeneous coordinate (x,y,z,w) and its image under a projective transform (x',y',z',w'), a projective transform has the following form:

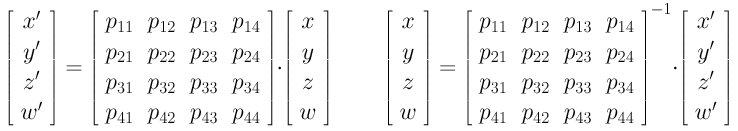
In the above, the 4-by-4 matrices must be non-singular (i.e., invertible). Therefore, projective transformations are more general than affine transformations because the fourth row does not have to contain 0, 0, 0 and 1.

Projective transformation can bring finite points to infinity and points at infinity to finite range. Let us take a look at an example. Consider the following projective transformation:

Obviously, this transformation sends (x,y,w)=(1,0,1) to (x',y',w') = (1,-1,0). That is, this projective transformation sends (1,0) on the xy-plane to the point at infinity in direction <1,-1>. From the right-hand side of the matrix equation x=Px' we have

x = 2x' + y'
y = x' + y'
w = 2x' + y' + w'

Let us consider a circle x^2 + y^2 = 1. Plugging the above equations into the circle equation changes it to the following:

x² + 2xy + y² - 4xw - 2yw - w² = 0

Dividing the above by w^2 to convert it back to conventional form yields

x² + 2xy + y² - 4x - 2y - 1 = 0

This is a parabola! (Why?) Therefore, a circle that has no point at infinity is transformed to a parabola that does have point at infinity.

While projective transformations, like affine transformations, do not change the degree of a polynomial, two parallel (i.e., intersecting) lines/planes can be transformed to two intersecting (i.e., parallel) lines/planes. Please verify this fact yourself.

Although we do not use these facts and the concept of projective transformations immediately, it will be very helpful in later lectures.

Matrix Multiplication and Transformations

We have introduced to you several transformations. We always show to you two forms, one from x to x' and the other the inverse from x' to x. In many cases, one may need several transformations to bring an object to its desired position. For example, one may need a transformation in matrix form q=Ap bringing p to q, followed by a second transformation r=Bq bringing q to r, followed by yet another transformation s=Cr bringing r to s. The net effect of p -> q -> r -> s can be summarized into a single transformation represented by the product of all involved matrices. Note that the first (resp., last) transformation matrix is the right-most (resp., left-most) in the multiplication sequence.

s = Cr = C(Bq) = CBq = CB(Ap) = CBAp

Therefore, to compute the net effect, we just compute CBA and use it as a single transformation, which brings p to s.

Let us take a look at an example. We want to perform the following transformations to an object:

Scale in the x-direction using a scale factor 5 (i.e., making it five times larger).
Followed by a rotation about z-axis 30 degree
Followed by a shear transformation in x- and y-direction with shearing factor 2 and 3, respectively.
Followed by a transformation moving the point in the direction of < 2, 1, 2 >.

Let the scaling, rotation, shearing and translation matrices be A, B, C and D, respectively. With previous discussion, we have the following, where matrix H = DCBA is the net effect:

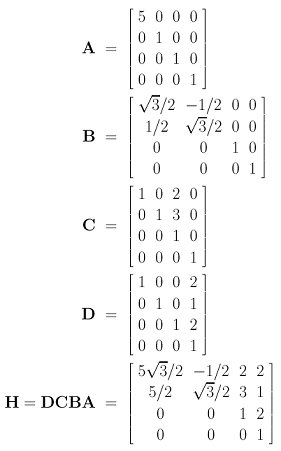
Therefore, the net effect of transforming a point x of the initial object to the corresponding point x' after the above four transformations is computed as x' = Hx = DCBAx.