Constructive Solid Geometry

Constructive Solid Geometry, or CSG for short, is yet another way of representing solids. A CSG solid is constructed from a few primitives with Boolean operators (i.e., set union, intersection and difference). Thus, a CSG solid can be written as a set equations and can also be considered a design methodology.

CSG Primitives

The standard CSG primitives consist of the block (i.e., cube), triangular prism, sphere, cylinder, cone and torus. These six primitives are in some normal or generic form and must be instantiated by the user to be used in his/her design. Moreover, the instantiated primitive may require transformations such as scaling, translation and rotation to be positioned at the desired place.

Suppose the block primitive is defined by its "lower left" corner < -1, -1, -1 > and "upper right" corner < 1, 1, 1 >. To produce a rectangular box with center at < 3, 2, 3 > and height and width 3 and length 5, a user may first scale the block primitive 1.5 times in the y- and z-direction and 2.5 times in the x-direction, and then translate the result to < 3, 2, 3 >. If the block primitive is called Block in a CSG system, the result may be obtained as follows:

translate(scale(Block, < 2.5, 1.5, 1.5 >), < 3, 2, 3 >)

In the above, the object to be transformed and the transformation data are the first and second arguments, respectively.

Boolean Operators

We can combined two instantiated and perhaps transformed primitives into one with set union, set intersection and set difference operators. However, simple set operators may create problems as will be discussed in regularized Boolean operators, modifications are required. Let us just use set operations on this page.

Given two sets, A and B, its union consists of all points from either A or B; its intersection consists of all points in both sets; and its difference, written as A - B (resp., B - A), consists of all points in A but not in B (resp., in B but not in A). In the following, A is the vertical cylinder and B is the horizontal cylinder. From left to right, the four solids are the union and intersection of A and B, A - B and B - A.

Therefore, a solid can be considered as the result of applying Boolean operators to a set of instantiated and transformed CSG primitives.

Let us take a look at a simple example. We want to design a bracket-like shape with a hole shown on the right-most figure below. We start with two instantiations of blocks and one instantiation of a cylinder (the left-most figure). Then, the two blocks are scaled and one of them is rotated to a vertical position. The cylinder is also scaled so that its radius matches that of the hole. These three instantiations are than transformed to their desired positions. The final product is obtained by computing the union of the two blocks and then subtracting from it the cylinder.

Please note that the design of the above solid is not unique. For example, the L shape can be constructed from subtracting a cube from another one.

CSG Expressions

The design procedure of the above bracket can be written as an expression:

diff(union(trans(Block1), trans(Block2)), trans(Cylinder))

where union(A,B) and diff(A,B) are the union and difference of A and B, and trans() indicates appropriate transformations. Or, if we use +, ^ and - for set union, intersection and difference, the above function calls can be rewritten as a set expression as follows:

(trans(Block1) + trans(Block2)) - trans(Cylinder)

This expression can be converted to an expression tree, the CSG Expression, of the design:

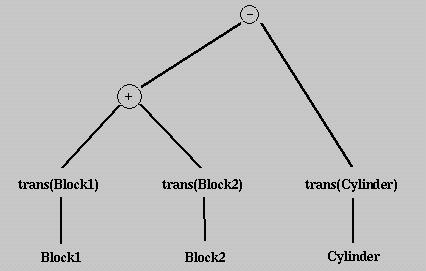
In fact, every solid constructed using the CSG technique has a corresponding CSG expression which in turn has an associated CSG tree. The expression of the CSG tree is a representation of the final design. Recall that the same solid may have different CSG expressions/trees. For example, one might punch a hole from Block1 first and then compute the union of this result with Block2. As a result, CSG representations are not unique.