
The surface of a solid must satisfy some conditions so that the resulting solid is well-behaved. This is the so-called manifold condition. While recent research has shown that the surface of a solid does not have to be a manifold, we shall restrict to manifold surfaces to simply our discussion.
A surface is a 2-manifold if and only if for each point x on the surface there exists an open ball with center x and sufficiently small radius so that the intersection of this ball and the surface can be continuously deformed to an open disk. An open ball with center at the coordinate origin and radius r is defined by equation x2 + y2 + z2 < r2. It contains all points inside of the sphere x2 + y2 + z2 = r2. An open disk is defined similarly x2 + y2 < r2. By continuously deformed, it means one can twist or bend the shape without cutting (i.e. adjacency relations must be maintained) and gluing (i.e. a one-to-one relation is required).
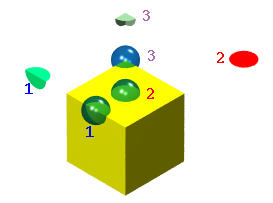
Let us take a look at the following figure:

There is a cube and three open balls. Ball 2 has its center on the top face. The intersection of this ball and the surface of the cube is an open disk (shown in red). Ball 1 has its center on an edge. Its intersection with the surface of the cube is a "bent" open disk, which of course can be "unbent" to make it an open disk. Ball 3 has its center at a corner. Its intersection with the cube's surface is a three-way bent open disk.
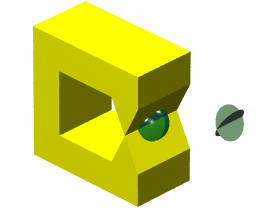
The following shows a solid whose bounding surface is not a manifold. The intersection of the open ball and the surface of the solid is the union of two intersecting open disks. This intersection cannot be deformed to an open disk without "gluing." Consequently, the surface is not a manifold.