Problems

1. Given a winged-edge representation of a solid, design algorithms to answer the following queries:
   • list all edges that contain a given vertex
   • list all faces that contains a given vertex
   • list all vertices and edges of a given face
2. Find the winged-edge data structure of a cube.
3. Find the winged-edge data structure of the following solid:
   

4. Find the winged-edge data structure of the following solid:
   

5. Verify Euler-Poincaré formula with the following polyhedra. List the number of vertices, edges, faces, loops, shells and holes.
   
6. Use Euler operators to construct the following polyhedra: (1) a cube, (2) a cube with "pothole" and (3) a cube with a penetrating hole. Figures for the last polyhedra can be found in the winged-edge problems.
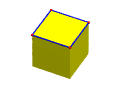
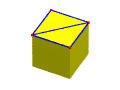
7. One can define a new operator MEFL in the Make group. This operator add an edge, a face and a loop. In general, this new edge subdivides a face into two, thus creating a new face and a new loop. In the following, the left one is a cube with vertices and edges of the top face shown. The right one is the result of apply an MEFL to the top face by adding an diagonal edge. The original square face is replaced by two triangles and F is increased by one. Similar, L is also increased by 1. Note that the value of the Euler-Poincaré formula does not change.
   

   One can use this operator MEFL to subdivide all faces into triangles.

   Use MEKL and MEFL to make all faces of a cube with a penetrate hole triangles. In the final result, do you have to worry about loops?

8. Starting with nothing, use Euler operators to construct a cube.