The Winged-Edge Data Structure

Perhaps the oldest data structure for a B-rep is Baumgart's winged-edge data structure. It is quite different from that of a wireframe model, because the winged-edge data structure uses edges to keep track almost everything. In what follows, we shall assume there is no holes in each face and later extend it to cope with holes. Moreover, we shall assume edges and faces are line segments and polygons. Topologically, one can always stretch curvilinear edges and faces so that they become flat without changing the relationships among them.

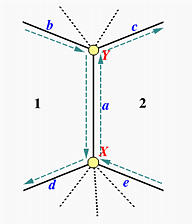
The above figure shows a polyhedron with vertices, edges and faces indicated with upper cases, lower cases and digits, respectively. Let us take a look at edge a = XY. This edge has two incident vertices X and Y, and two incident faces 1 and 2. A face is a polygon surrounded by edges. For example, face 1 has its edges a, c and b, and face 2 has its edges a, e and d. Note that the ordering is clockwise viewed from outside of the solid. If the direction of the edge is from X to Y, faces 1 and 2 are on the right and left side of edge a, respectively. To capture the ordering of edges correctly, we need four more pieces of information. Since edge a is traversed once when traversing face 1 and traversed a second time when traversing face 2, it is used twice in different directions. For example, when traversing the edges of face 1, the predecessor and successor of edge a are edge b and edge c, and when traversing the edges of face 2, the predecessor and successor of edge a are edge d and edge e. Note that although there are four edges incident to vertex X, only three of them are used when finding faces incident to edge a. Therefore, for each edge, the following information are important:

vertices of this edge,
its left and right faces,
the predecessor and successor of this edge when traversing its left face, and
the predecessor and successor of this edge when traversing its right face.

The Edge Table

Each entry in the edge table contains those information mentioned earlier: edge name, start vertex and end vertex, left face and right face, the predecessor and successor edges when traversing its left face, and the predecessor and successor edges when traversing its right face. Note that clockwise ordering (viewing from outside of the polyhedron) is used for traverse. Note also that the direction of edge a is from X to Y. If the direction is changed to from Y to X, all entries but the first one in the following table must be changed accordingly.

*Edge*	*Vertices*		*Faces*		*Left Traverse*		*Right Traverse*
*Name*	*Start*	*End*	*Left*	*Right*	*Pred*	*Succ*	*Pred*	*Succ*
a	X	Y	1	2	b	d	e	c

The above shows the information for the entry of edge a. The four edges b, c, d and e are the wings of edge a and hence edge a is "winged."

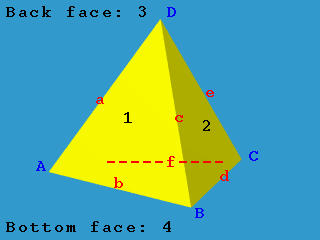
The above is a tetrahedron with four vertices A, B, C and D, six edges a, b, c, d, e and f, and four faces 1, 2, 3 (back) and 4 (bottom). Its edge table is the following. Please use the above diagram to verify this table.

*Edge*	*Vertices*		*Faces*		*Left Traverse*		*Right Traverse*
*Name*	*Start*	*End*	*Left*	*Right*	*Pred*	*Succ*	*Pred*	*Succ*
a	A	D	3	1	e	f	b	c
b	A	B	1	4	c	a	f	d
c	B	D	1	2	a	b	d	e
d	B	C	2	4	e	c	b	f
e	C	D	2	3	c	d	f	a
f	A	C	4	3	d	b	a	e

Other Tables

The winged-edge data structure requires two more tables, the vertex table and the face table. These two are very simple. The vertex table has one entry for each vertex which contains an edge that is incident to this vertex. The face table has one entry for each face which contains an edge that is one of this face's boundary edges. Therefore, we have the following table. Note that since there are multiple choices of edges, you may come up with different tables:

*Vertex Name*	*Incident Edge*
A	a
B	b
C	d
D	e

*Face Name*	*Incident Edge*
1	a
2	c
3	a
4	b

With this data structure, one can easily answer the question: which vertices, edges, faces are adjacent to each face, edge, or vertex. There are nine of these adjacency relations. For example, is vertex X adjacent to face 5? Are faces 3 and 5 adjacent to each other? The winged-edge data structure can answer these queries very efficiently and some of them may even be answered in constant time. However, it may take longer time to answer other adjacency queries. Note also that once the numbers of vertices, edges and faces are known, the size of all three tables are fixed and will not change.

What If Faces Have Holes?

If some faces of a solid have holes, the above form of winged-edge data structure does not work. These holes may penetrate the solid (the left box below) or just like a pothole (the right box below).

There are two ways for resolving this problem:

For a face with inner loops, the outer boundary is ordered clockwise, while its inner loops, if any, are ordered counter clockwise.
Another simple method is adding an auxiliary edge between each inner loop and the outer loop as shown below. This auxiliary edge will have the same face for its left and right faces. In this way, a face with holes becomes a single loop which can be represented with the winged-edge data structure. When traversing a loop, auxiliary edges can be identified easily since its left and right faces are the same.