Problems

1. Show that a degree n two-variable polynomial has (n+1)(n+2)/2 terms and that a degree n three-variable polynomial has (n+1)(n+2)(n+3)/6 terms.
2. Under finite precision arithmetic, addition and multiplication operators are commutative. In general, the associative law and distributive law do not hold. Suppose you have a decimal computer with four significant digits for floating number computation.
   • Find three floating point numbers a, b and c such that (a*b)*c is not equal to a*(b*c). That is, the associative law fails.
   • Find three floating point numbers a, b and c such that a*(b+c) is not equal to a*b+a*c. That is, the distributive law fails.
3. Function cos(x) has a series similar to that of sin(x):
   

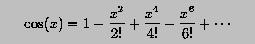
   Based on the function of sin(x), write a function for cos(x). Will you get strange results similar to that of sin(x).

4. Let us minimize the effect of subtractions in the computation of sin(x) and cos(x). Use two variables, positive and negative. The former accumulates all terms with positive signs, while the latter accumulates all terms with negative signs. The result is positive - negative. Would this scheme be better? Write a program to verify it.
5. Given a polynomial like the following one:
   

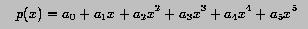
   it is always possible to rearrange the terms to a new form:

   

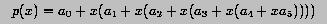
   What is the advantages of the second form over the first one? Please count the number of multiplications. Which form would propagate errors faster? Write a function that takes a degree n polynomial (coefficients in an array) and an x, and evaluates the polynomial at x using the second form.

6. Let us do a dramatic floating point computation experiment.
   

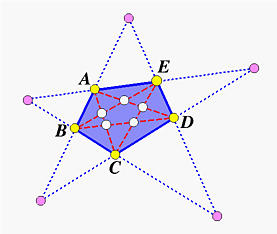
   The above shows a pentagon ABCDE. If we draw the five diagonals of this pentagon, we have a smaller pentagon lying in pentagon ABCDE. This smaller pentagon has its vertices in white color. Let us call the original pentagon P and the smaller pentagon in(P), because it is the result of "going" inside of pentagon P.

   If we extend the sides of the given pentagon, they will intersect in five points, which define a new pentagon lying outside of pentagon P. We call this new "outside" pentagon out(P), because it lies outside of pentagon P.

   From this construction, we know that going out from in(P) should be P. Similarly, going in from out(P) should also be P. More precisely, we have P = out(in(P)) and P = in(out(P)). Let in^k(P) denote executing the "going in" operation k times, and out^k(P) denote executing the "going out" operation k times. Then, the following should hold

   P = out^k(in^k(P)) = in^k(out^k(P))

   This means that going in k times followed by going out k times should yield pentagon P. Similarly, going out k times followed by going in k times should also yield pentagon P.

   Now consider the following strange pentagon:

   

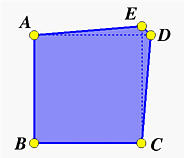
   The vertices are as follows, where p can be 0.1, 0.01, 0.001, 0.0001, 0.00001 and 0.000001.

   Vertex	x	y
   A	0	1
   B	0	0
   C	1	0
   D	1 + p	1
   E	1	1 + p

   For a given P, compute out²(in²(P)), out³(in³(P)), in²(out²(P)) and in³(out³(P)). Then, theoretically all four pentagons should be identical to pentagon P. Unfortunately, due to finite precision arithmetic, this is not the case. As a result, we should measure the error generated from the in() and out() operations. For each vertex of the pentagon P, say A = (x, y), and its corresponding result after taking the in() and out() operations, say A' = (x', y'), we compute the maximum error as follows:

   maximum error of A = maximum of |x - x'| and |y - y'|

   The maximum error of P is the maximum over all five vertices. Then, you can compile a table as follows:

   p	out2(in2(P))	out3(in3(P))	in2(out2(P))	in3(out3(P))
   0.1	fill maximum error in each entry
   0.01
   0.001
   0.0001
   0.00001
   0.000001

   Write a program that uses both float and double to perform the calculation and generate the above max. error table. Name your program pentagon.c. You will need (1) constructing a line from two points, and (2) computing the intersection point of two lines. Please consult your calculus and analytic geometry book. Then, use your program to do the following: (1) filling the required max. error table, (2) generating the vertices of the resulting pentagons, and (3) producing an analysis for the following questions: (a) why could the error be very large? (b) will you be able to pinpoint the potential problem(s)? (c) which vertex (or vertices) causes the largest error?, and (d) any findings that are worth mentioning.