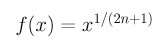The Theme of this Course

Going from a geometric concept/problem to a working program usually takes several steps as follows:

Geometry -> Algebra -> Algorithm -> Program

Since computers do not understand geometry, one must convert a geometric problem to an algebraic one that uses numbers. Then, one can design algorithms to manipulate these numbers and finally, programs are developed based on these algorithms. However, each step is a difficult and challenging task.

Geometry -> Algebra

When we think about a geometric object, even a simple one such as a point or a line, we normally have its shape in mind. But, to have computers to process a geometric object, we have to find a representation for that object so that it can be described in a form that can be manipulated by computers. For example, a point in three-dimensional space is represented with three numbers like (2.5, 0.0, -4.0), and a line in the xy-coordinate plane has an equation like 3x - 5.3y + 3 = 0.

A geometric object's representation is usually not unique. A circle can be represented by an implicit equation:

x² + y² = 1

or in a parametric form using trigonometric functions:

x = cos(t)
y = sin(t)

where t is in the range of 0 and 360 degree.

Some geometric objects such as polyhedra many even require complex data structures to represent all of its details. Therefore, finding a good and appropriate representation (for a particular application) is usually a very challenging task. We shall cover some of these representations in this course. Some are mathematical (for curves and surfaces) and some are combinatorial (for polyhedra). Whatever representation is chosen, it must be easy to use and manipulate, and support all desired operations efficiently and accurately.

In addition to a representation for a particular type of geometric objects, one must convert geometric operations to algebraic forms, too. Take a look at the following question. Given a sphere of radius r, what is the locus of this sphere if its center moves on a curve? We know that the locus, usually referred to as a sweep, looks like a tube; but, it is not so easy to know what exactly this tube looks like. If the curve is a line, the locus is a cylinder. The difficult part is that the curve is not a line and/or that the radius of the given sphere can change. Therefore, we have an easily described geometric operation whose algebraic counterpart is somewhat complicated.

Algebra -> Algorithm

After finding representations for geometric objects and algebraic interpretations for your geometric operations, the next step is to find algorithms for manipulating the representations and equations. Is it easy? Sometimes it is. For example, if the problem is "determine if two lines on the xy-coordinate plane intersect and if they are, find the intersection point," it can be solved easily. Let the lines be

Ax + By + C = 0
Ux + Vy + W = 0

Then, if they are parallel to each other (i.e., A*V=B*U), there is no intersection point; otherwise, the intersection point can be found by solving the above simultaneous linear equations of two variables.

Unfortunately, other practical problems are not so easy. First, the representation of a geometric object such as a piston engine or the Boeing 777 is huge and the number of equations, usually non-linear ones with many variables, is also huge. Manipulating these representations and equations is not an easy job. However, we have at least the following choices:

Symbolic Computation
A symbolic system delivers symbolic answers. For example, if you ask a symbolic system to solve a quadratic equation Ax² + Bx + C =0, it would give you the following equations of roots:

root1 = (-B + SQRT(B²-4*A*C))/(2*A)
root2 = (-B - SQRT(B²-4*A*C))/(2*A)
Therefore, the answers are algebraic rather than numerical. There are good symbolic systems available (e.g., Mathematica and Maple). Computation cost is usually very high (e.g. very slow). On the other hand, symbolic computation is able to give you a closed-form solution, a form that can be written in one or more formulae.
Numerical Computation
Numerical solutions give you a bunch of numbers rather than a closed-form solution. Numerical computation has been a popular way of finding solutions for geometric problem. For example, in calculus you perhaps have learned Newton's method for solving non-linear equation. The solution is merely a number. Numerical computation is fast; but, since computers cannot represent real numbers exactly, extreme care must be taken to avoid loss of significant digits and other related problems. For example, if the initial guess for Newton's method is incorrect, you may not be able to find a root. As a suggestion, please try to solve the following equation using Newton's method:

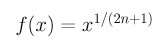
where n is a positive integer. This equation has a root at zero. But, Newton's method will not converge to zero at all. Try it yourself.
Approximation
Since symbolic computation is time consuming and numerical computation sometime does not deliver the result, let us take a compromise. Let us simplify our solution by only asking for a good approximation. For example, it is provably true that in general a polynomial with degree higher than four does not have any closed-form solution. Numerical methods (e.g. Newton's method) can only give us an approximation of the roots of a higher degree polynomial. So, the question is "how good is good." This is obviously problem dependent. We shall return to this question later on.

The above does not enumerate all possibilities. One can combine several ways together to solve a single problem. For example, one can use symbolic to solve some parts of the problem and use a combination of numerical computation and approximation to do the remaining.

Recently, some authors suggested the so-called geometric methods whose fundamental merit involves characterizing the results using geometry reasoning and using the characterization for calculating the result. This method usually work fine with simple problems and may require a large number of case-by-case analysis. However, if geometric method works, it usually delivers the solution fast and is more accurate and robust than other methods. We will not pursue in this direction in this course.

Algorithm -> Program

Ok, you might want to say that, after all of the troubles in the previous steps, we have algorithms and therefore writing program should be easy. No, it is not always the case. Translating some algorithms in your algorithms design textbook to programs may be easy. Translating geometric algorithms to programs requires extreme care. There are geometric programming languages. Even though you have had all the helps from a programming system, its debugger and graphics library, you still have to be very careful about the problem of real number computations. Computation errors and loss of significant digits may occur easily and in many cases their impacts may be propagated and amplified. As a result, a theoretically sound algorithm may deliver meaningless results. You may have learned this in a numerical methods course; but, I will reiterate this issue later on to emphasize its importance in geometric computation.

In this course, we shall introduce several representations for curves, surfaces and solids and their accompanying geometric operations. We shall spend a considerable amount of time on curves and surfaces design using approximation. Another point we want to emphasize is the impact of floating number computations on geometric problems. Some classical computational geometry problems will also be mentioned, because they are useful and can illustrate what computational geometers are doing.