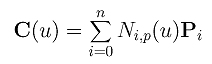

Although B-spline curves are more complicated than Bézier curves, their derivatives share a very similar form. Suppose a B-spline curve is defined as follows:
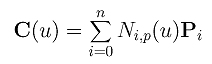
The derivative of each of these basis functions can be computed as follows:
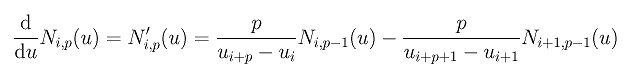
Plugging these derivatives back to the curve equation yields the following result:
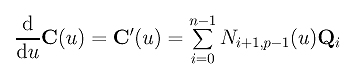
where Qi's are defined as follows:
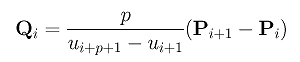
Therefore, the derivative of a B-spline curve is another B-spline curve of degree p - 1 on the original knot vector with a new set of n control points Q0, Q1, ..., Qn-1.
If the original clamped knot vector is
u0(p+1), up+1, ...,
um-p-1, um(p+1), then
removing the first and the last knots so that the multiplicity of the first
and the last knots become p rather than p+1, we have a new
knot sequence of m - 1 knots
u0(p), up+1, ...,
um-p-1, um(p).
Then, it can be shown that
Ni+1,p-1(u)
evaluated on the original knot sequence is equal to
Ni,p-1(u) on the new one.
Therefore, on the new knot sequence the derivative of a B-spline curve is
the following:
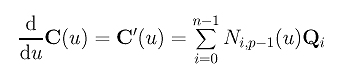
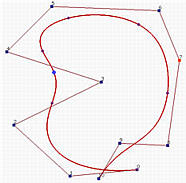
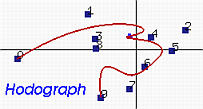
In the following left is a B-spline curve of degree 5. Its derivative curve, which is a B-spline curve of degree p-1 defined by the new n control points, is shown in the middle. As in the Bézier curve case, this is the hodograph of the original curve. Below right shows the same hodograph with control polyline removed.


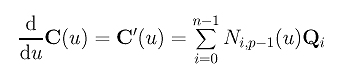
whose knot vector is obtained by dropping the first knot and last knot from the original knot sequence. Thus, the multiplicity of the first (and of course the last) knot is p and, consequently, the above B-spline curve of degree p-1 is clamped. Since a clamped B-spline curve passes through its first and last control points, we have C'(0) = Q0 and C'(1) = Qn-1. Since u0 = .... = up = 0 for i = 0, we have
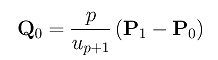
Therefore, the tangent vector at C'(0) is in the same direction of the vector from P0 to P1 and C(u) is tangent to the first leg.
With the same reasoning, we can show the following:
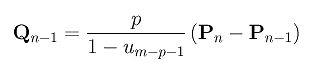
Hence, C(u) is tangent to the last leg. In summary, we have the following important fact:
| A clamped B-spline curve passes through the first and last control points and is tangent to the first and last legs of the control polyline. |
