B-spline Basis Functions: Computation Examples

Two examples, one with all simple knots while the other with multiple knots, will be discussed in some detail on this page.

Simple Knots

Suppose the knot vector is U = { 0, 0.25, 0.5, 0.75, 1 }. Hence, m = 4 and u0 = 0, u1 = 0.25, u2 = 0.5, u3 = 0.75 and u4 = 1. The basis functions of degree 0 are easy. They are N0,0(u), N1,0(u), N2,0(u) and N3,0(u) defined on knot span [0,0.25,), [0.25,0.5), [0.5,0.75) and [0.75,1), respectively, as shown below.

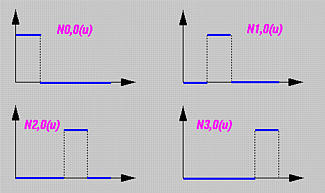
The following table gives the result of all Ni,1(u)'s:

Basis Function Range Equation
N0,1(u) [0, 0.25) 4u
[0.25, 0.5) 2(1 - 2u)
N1,1(u) [0.25, 0.5) 4u - 1
[0.5, 0.75) 3 - 4u
N2,1(u) [0.5, 0.75) 2(2u - 1)
[0.75, 1) 4(1 - u)

The following shows the graphs of these basis functions. Since the internal knots 0.25, 0.5 and 0.75 are all simple (i.e., k = 1) and p = 1, there are p - k + 1 = 1 non-zero basis function and three knots. Moreover, N0,1(u), N1,1(u) and N2,1(u) are C0 continuous at knots 0.25, 0.5 and 0.75, respectively.

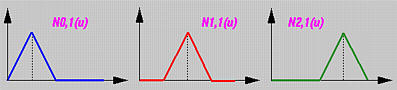
From Ni,1(u)'s, one can compute the basis functions of degree 2. Since m = 4, p = 2, and m = n + p + 1, we have n = 1 and there are only two basis functions of degree 2: N0,2(u) and N1,2(u). The following table is the result:

Basis Function Range Equation
N0,2(u) [0, 0.25) 8u2
[0.25, 0.5) -1.5 + 12u - 16 u2
[0.5, 0.75) 4.5 - 12u + 8 u2
N1,2(u) [0.25, 0.5) 0.5 - 4u + 8u2
[0.5, 0.75) -1.5 + 8u - 8u2
[0.75, 1) 8(1 - u)2

The following figure shows the two basis functions. The three vertical blue lines indicate the positions of knots. Note that each basis function is a composite curve of three degree 2 curve segments. For example, N0,2(u) is the green curve, which is the union of three parabolas defined on [0,0.25), [0.25, 0.5) and [0.5,0.75). These three curve segments join together forming a smooth bell shape. Please verify that N0,2(u,) (resp., N1,2(u)) is C1 continuous at its knots 0.25 and 0.5 (resp., 0.5 and 0.75). As mentioned on the previous page, at the knots, this composite curve is of C1 continuity.

Knots with Positive Multiplicity

If a knot vector contains knots with positive multiplicity, we will encounter the case of 0/0 as will be seen later. Therefore, we shall define 0/0 to be 0. Fortunately, this is only for hand calculation. For computer implementation, there is an efficient algorithm free of this problem. Furthermore, if ui is a knot of multiplicity k (i.e., ui = ui+1 = ... = ui+k-1), then knot spans [ui,ui+1), [ui+1,ui+2), ..., [ui+k-2,ui+k-1) do not exist, and, as a result, Ni,0(u), Ni+1,0(u), ..., Ni+k-1,0(u) are all zero functions.

Consider a knot vector U = { 0, 0, 0, 0.3, 0.5, 0.5, 0.6, 1, 1, 1 }. Thus, 0 and 1 are of multiplicity 3 (i.e., 0(3) and 1(3)) and 0.5 is of multiplicity 2 (i.e., 0.5(2)). As a result, m = 9 and the knot assignments are

u0 u1 u2 u3 u4 u5 u6 u7 u8 u9
0 0 0 0.3 0.5 0.5 0.6 1 1 1

Let us compute Ni,0(u)'s. Note that since m = 9 and p = 0 (degree 0 basis functions), we have n = m - p - 1 = 8. As the table below shows, there are only four non-zero basis functions of degree 0: N2,0(u), N3,0(u), N5,0(u) and N6,0(u).

Basis Function Range Equation Comments
N0,0(u) all u 0 since [u0, u1) = [0,0) does not exist
N1,0(u) all u 0 since [u1, u2) = [0,0) does not exist
N2,0(u) [0, 0.3) 1
N3,0(u) [0.3, 0.5) 1
N4,0(u) all u 0 since [u4, u5) = [0.5,0.5) does not exist
N5,0(u) [0.5, 0.6) 1
N6,0(u) [0.6, 1) 1
N7,0(u) all u 0 since [u7, u8) = [1,1) does not exist
N8,0(u) all u 0 since [u8, u9) = [1,1) does not exist

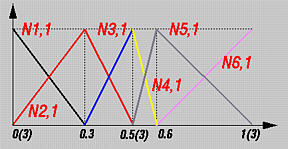
Then, we proceed to basis functions of degree 1. Since p is 1, n = m - p - 1 = 7. The following table shows the result:

Basis Function Range Equation
N0,1(u) all u 0
N1,1(u) [0, 0.3) 1 - (10/3)u
N2,1(u) [0, 0.3) (10/3)u
[0.3, 0.5) 2.5(1 - 2u)
N3,1(u) [0.3, 0.5) 5u - 1.5
N4,1(u) [0.5, 0.6) 6 - 10u
N5,1(u) [0.5, 0.6) 10u - 5
[0.6, 1) 2.5(1 - u)
N6,1(u) [0.6, 1) 2.5u - 1.5
N7,1(u) all u 0

The following figure shows the graphs of these basis functions.

Let us take a look at a particular computation, say N1,1(u). It is computed with the following expression:

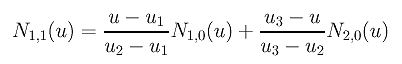
Plugging u1 = u2 = 0 and u3 = 0.3 into this equation yields the following:

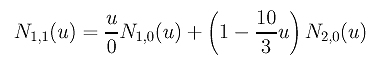
Since N1,0(u) is zero everywhere, the first term becomes 0/0 and is defined to be zero. Therefore, only the second term has an impact on the result. Since N2,0(u) is 1 on [0,0.3), N1,1(u) is 1 - (10/3)u on [0,0.3).

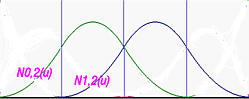
Next, let us compute all Ni,2(u)'s. Since p = 2, we have n = m - p - 1 = 6. The following table contains all Ni,2(u)'s:

Basis Function Range Equation
N0,2(u) [0, 0.3) (1 - (10/3)u)2
N1,2(u) [0, 0.3) (20/3)(u - (8/3)u2)
[0.3, 0.5) 2.5(1 - 2u)2
N2,2(u) [0, 0.3) (20/3)u2
[0.3, 0.5) -3.75 + 25u - 35u2
N3,2(u) [0.3, 0.5) (5u - 1.5)2
[0.5, 0.6) (6 - 10u)2
N4,2(u) [0.5, 0.6) 20(-2 + 7u - 6u2)
[0.6, 1) 5(1 - u)2
N5,2(u) [0.5, 0.6) 20u2 - 20u + 5
[0.6, 1) -11.25u2 + 17.5u - 6.25
N6,2(u) [0.6, 1) 6.25u2 - 7.5u + 2.25

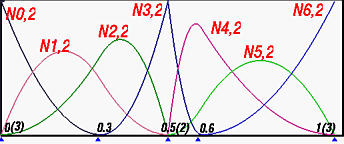
The following figure shows all basis functions of degree 2.

Let us pick a typical computation as an example, say N3,2(u). The expression for computing it is

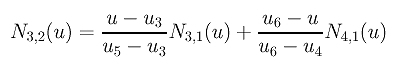
Plugging in u3 = 0.3, u4 = u5 = 0.5 and u6 = 0.6 yields

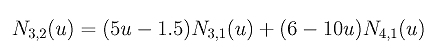
Since N3,1(u) is non-zero on [0.3, 0.5) and is equal to 5u - 1.5, (5u - 1.5)2 is the non-zero part of N3,2(u) on [0.3, 0.5). Since N4,1(u) is non-zero on [0.5, 0.6) and is equal to 6 - 10u, (6 - 10u)2 is the non-zero part of N3,2(u) on [0.5, 0.6).

Let us investigate the continuity issues at knot 0.5(2). Since its multiplicity is 2 and the degree of these basis functions is 2, basis function N3,2(u) is C0 continuous at 0.5(2). This is why N3,2(u) has a sharp angle at 0.5(2). For knots not at the two ends, say 0.3, C1 continuity is maintained since all of them are simple knots.