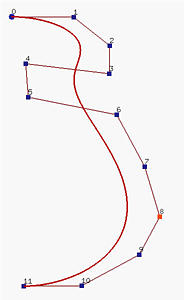

Consider designing the profile of a vase. The left figure below is a Bézier curve of degree 11; but, it is difficult to bend the "neck" toward the line segment P4P5. Of course, we can add more control points near this segment to increase the weight to that region. However, this will increase the degree of the curve. In many cases, it is not worth to use such a high degree polynomial.



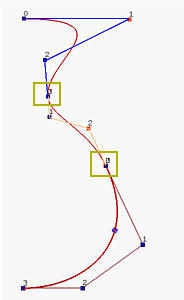
As discussed in a previous page about the derivatives of a Bézier curve, we can join two Bézier curves together. As long as the last leg of the first curve and the first leg of the second have the same direction, we can at least achieve G1 continuity because the tangent vectors have the same direction but may have different length (i.e., if the lengths are the same, it becomes C1 continuous). The middle figure above uses this idea. It has three Bézier curve segments of degree 3 with joining points marked with yellow rectangles. This shows that with multiple low degree Bézier curve segments satisfying the G1 continuous condition, we still can design complex shapes. But, maintaining this G1 continuous condition may be tedious and undesirable.
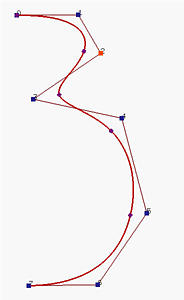
Is it possible that we still can use lower degree curve segments without worrying about the G1 continuous condition? B-spline curves are generalizations of Bézier curves and are developed to answer this question. The right figure above is a B-spline curve of degree 3 defined by 8 control points. In fact, there are five Bézier curve segments of degree 3 joining together to form the B-spline curve defined by the control points. In the above, those little dots subdivide the B-spline curve into Bézier curve segments. One can move control points for modifying the shape of the curve just like what we do to Bézier curves. We can also modify the subdivision of the curve. Therefore, B-spline curves have higher degree of freedom for curve design.
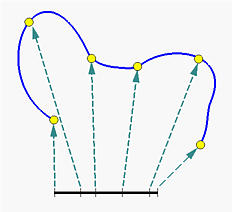
Subdividing the curve directly is difficult to do. Instead, we subdivide the domain of the curve. Thus, if the domain of a curve is [0,1], this closed interval is subdivided by points called knots. Let these knots be 0 <= u0 <= u1 <= ... <= um <= 1. Then, points C(ui)'s subdivide the curve as shown in the figure below and, consequently, modifying the subdivision of [0,1] changes the shape of the curve.
In summary, to design a B-spline curve, we need a set of control points, a set of knots and a set of coefficients, one for each control point, so that all curve segments are joined together satisfying certain continuity condition. The computation of the coefficients is perhaps the most complex step because they must ensure certain continuity conditions. Fortunately, this computation is usually not needed in this course. We only need to know their characteristics for reasoning about B-spline curves.