B-spline Curves: Inserting a Knot Multiple Times

In many applications, a knot is required to be inserted multiple times. A simple method for inserting the same knot multiple times is to repeatedly apply the knot insertion algorithm. However, in doing so, the original knot vector and the original set of control points must be modified after each insertion, which is a rather tedious task. Fortunately, by studying the behavior of the knot insertion algorithm, we can find a much simpler way to do the same.

Observation I: The Coefficients for Computing the New Control Points

Let us start with a simple case. Let t be inserted in the middle of knot span [u_k, u_k+1) and let the degree be p. The coefficients a_i,1's for the first insertion, where k-p+1 <= i <= k, are computed as follows:

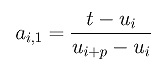
After t is inserted, it becomes a knot and knots u_k+1, u_k+2, ..., u_m will be shifted one position to the right. More precisely, the new knots, v₀, v₁, ..., v_k, v_k+1, ..., v_m and v_m+1 are

Note that v_k+1 divides the new knot vector into two halves. Knots to the left of v_k+1 = t are identical to the corresponding values of the original, while knots to the right of t satisfy the relation v_h = u_h-1.

If t is inserted again, it lies in knot span [v_k+1,v_k+2). Since t is equal to the left end, this second insertion makes v_k+1 a double knot. The coefficients a_i,2's for this second insertion, based on the new knot sequence, are computed as

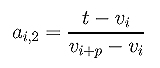
where i is less than or equal to k+1. Rewriting the above using u we have

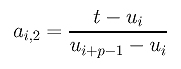
Note that the u_i's are on the left-hand side of t = v_k+1 and the u_i+p's are on the right-hand side of v = v_k+1.

Let this new set of knots be w_i's. The relation of this new set and the origin is shown below:

Let t be inserted a third time, which makes w_k+1 a triple knot. It is not difficult to see that the coefficients a_i,3's for this third insertion are computed as follows:

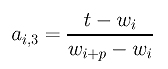
The above can be rewritten as

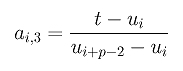
Generalizing this idea, a_i,h's, the coefficients for the h-th insertion, are computed as follows:

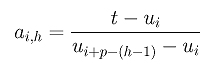
What if in the original knot vector u_k is a multiple knot with multiplicity s and t is inserted at u_k? Would this affect the above formula? Fortunately, nothing will change. Let us see why. If u_k is a multiple knot of multiplicity s, then u_k = u_k-1 = u_k-2 = ... = u_k-s+1:

Because all of them lie to the left-hand side of t and because the shifting of indices only happen to those knots to right of t, the computation formula for a_i,h does not have to be modified. Therefore, we conclude that

If a new knot t is inserted to knot span [uk, uk+1) h times, the coefficients ai,h can be computed as follows:

Observation II: The Computation of New Control Points

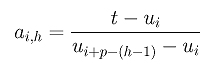
Recall from the way of inserting a knot at an existing knot that if t is inserted at an existing knot u_k of multiplicity s, then control points P_k-s, P_k-s+1, ..., P_k-1 and P_k are not affected and only P_k-p, P_k-p+1, ..., P_k-s participate in the computation of new control points Q_i's. Let us rewrite all new control points after the first insertion with a second subscript 1. Thus, we have the following diagram:

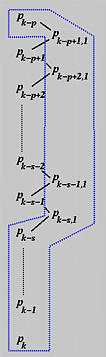
If the same knot is inserted the second time, the affected p+1 control points are P_k, P_k-1, P_k-s, P_k-s,1, P_k-s-1,1, ..., P_k-p+1,1 as shown in the above diagram. Note that P_k-p is excluded because only p+1 control points are affected. However, since the multiplicity of t is increased by one due to the previous insertion, s+2 control points will not participate in the knot insertion computation: P_k, P_k-1, ..., P_k-s and P_k-s,1. The computation scheme and the new set of control points are shown below. Note that new control points generated from the second insertion has 2 as the second subscript. The new control points are: (1) P_k-p+1,1 and P_k-s,1 computed from the first insertion, and (2) P_k-p+2,2 to P_k-s,2 computed from the second insertion.

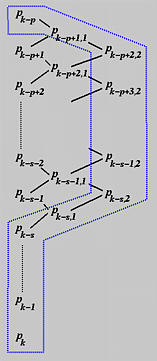
For the third insertion, the affected p+1 control points are P_k-p+2,2 to P_k-s,2, P_k-s,1, and P_k-s to P_k. Since this third insertion increases the multiplicity of t by one again, the number of control points that will not involve in the computation is also increased by one. As a result, P_k-s,2 will be the same before and after the third insertion. This is the meaning of the following diagram:

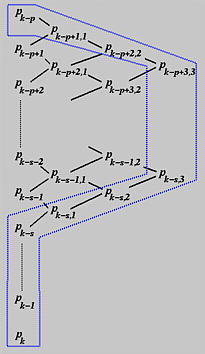
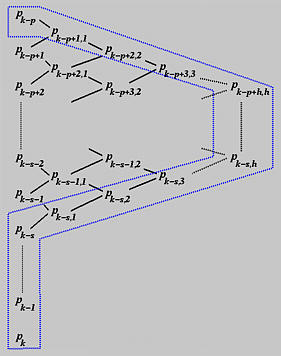
In general, if t is inserted h times at a knots u_k of multiplicity s, where s = 0 means t is inserted in the middle of that knot span and s > 0 means t is inserted at a knot u_k of multiplicity s, one can

1. write down the first set of p+1 affected control points as the 0-th column;
2. ignore the last s control points (i.e., P_k-s+1 to P_k);
3. compute the first column, the second column, ... and the h-th column;
4. the new set of control points are those surrounded by the blue polygon

A Summary

Combining these two observations, we have the following algorithm for inserting a knot t multiple times.

Input: knot t in [u_k, u_k+1) with initial multiplicity s to be inserted h times, where h+s is less than or equal to p, the degree of the given B-spline curve
Output: a new set of control points after t is inserted h times

Let control points P_k, P_k-1, ..., P_k-p be renamed as P_k,0, P_k-1,0, ..., P_k-p,0 by adding a second subscript 0.

for r := 1 to h do

for i := k-p+r to k-s do

begin

Let a_i,r = (t - u_i) / ( u_i+p-r+1 - u_i )
Let P_i,r = (1 - a_i,r) P_i-1,r-1 + a_i,r P_i,r-1

end


The new set of control points are constructed from the original ones from P₀ to P_k-p, followed by the top edge of the diagram above (i.e., P_k-p+1,1, P_k-p+2,2, ..., P_k-p+h,h), followed by the right edge of the diagram (i.e., P_k-p+h+1,h, P_k-p+h+2,h, ...., P_k-s,h), followed by the bottom edge of the diagram (i.e., P_k-s,h-1, P_k-s,h-2, ...., P_k-s,1), followed by the original control points P_k-s, ..., P_k, ..., P_n.

Corner Cutting

As mentioned earlier, knot insertion is a corner cutting process. For example, suppose we have a B-spline curve of degree 6 and want to insert u twice at a knot u₁₀ of multiplicity 2. The affected control points are P₁₀, P₉, ..., P₄, since k = 10, p = 6 and k-p = 4. Since the multiplicity of u₁₀ is 2, we have s = 2 and u₁₀ and P₉ are not changed. The first insertion produces P_8,1, P_7,1, P_6,1 and P_5,1 and the corners at P₇, P₆ and P₅ are cut. The new set of control points contains P₀ to P₄, P_5,1, P_6,1, P_7,1, P_8,1, P₈, P₉, P₁₀, .....

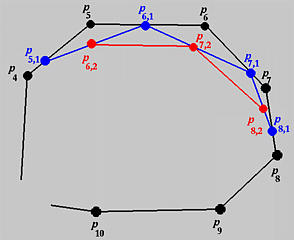
The second insertion produces P_8,2, P_7,2 and P_6,2. Thus, the corners at P_7,1 and P_6,1 are cut and the new set of control points are P₀ to P₄, P_5,1, P_6,2, P_7,2, P_8,2, P_8,1, P₈, P₉, P₁₀, .....