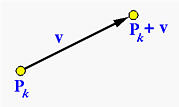

Changing the position of a control point will change the shape of the defined Bézier curve. Our question is:
| How does the shape of the curve change if a control point is moved to a new position? |
Suppose a control point Pk is moved to a new position Pk + v, where vector v gives both the direction and length of this move. This is shown as follows:

Let the original Bézier curve be as follows:
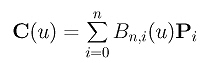
Since the new Bézier curve is defined by P0, P1. ..., Pk+v, ..., Pn, its equation D(u) is
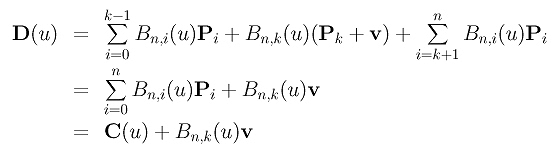
In the above, since only the k-th term uses a different control point Pk + v, after regrouping we know that the new curve is the sum of the original curve and an extra term Bn,k(u)v. This means:
| The corresponding point of u on the new curve is obtained by translating the corresponding point of u on the original curve in the direction of v with a distance of |Bn,k(u)v|. |
More precisely, given a u, we have point C(u) on the original curve and D(u) on the new curve and D(u) = C(u) + Bn,k(u)v. Since v gives the direction of movement, D(u) is the result of moving C(u) in the same direction. The length of this translation is, of course, the length of vector Bn,k(u)v. Therefore, when Bn,k(u) reaches its maximum, the change from C(u) to D(u) is the largest.
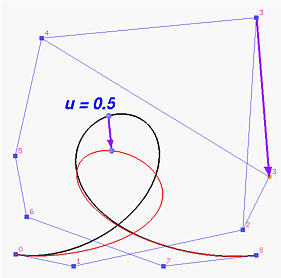
The following figure illustrates this effect. Both the black and red curves are Bézier curves of degree 8 defined by 9 control points. The black one is the original curve. If its control point 3 is moved to a new position as indicated by the blue vector, the black curve changes to the red one. On each of these two curves there is the point corresponding to u=0.5. It is clear that C(0.5) moves in the same direction to D(0.5). The distance between C(0.5) and D(0.5) is the length of vector B8,3(0.5)v = 8!/(3!(8-3)!)×0.53(1-0.5)8-3v = 0.22v. Hence, the distance is about 22% of the distance between the original control point 3 and the new control point 3 as shown in the figure below.
We can obtain one more important conclusion from the above discussion. Since Bn,k(u) is non-zero in the open interval (0,1), Bn,k(u)v is not a zero vector in (0,1). This means that except for the two endpoints C(0) and C(1) all points on the original curve are moved to new locations. Therefore, we have
| Changing the position of a control point causes the shape of a Bézier curve to change . |