Subdividing a Bézier Curve

The meaning of subdividing a curve is to cut a given Bézier curve at C(u) for some u into two curve segments, each of which is still a Bézier curve. Because the resulting Bézier curves must have their own new control points, the original set of control points is discarded. Moreover, since the original Bézier curve of degree n is cut into two pieces, each of which is a subset of the original degree n Bézier curve, the resulting Bézier curves must be of degree n.

Our problem is:

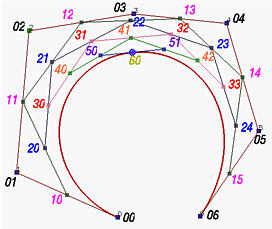
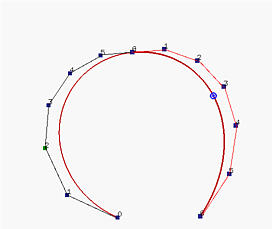
Given a set of n + 1 control points P0, P1, P2, ..., Pn and a parameter value u in the range of 0 and 1, we want to find two sets of n+1 control points Q0, Q1, Q2, ..., Qn and R0, R1, R2, ..., Rn such that the Bézier curve defined by Qi's (resp., Ri's) is the piece of the original Bézier curve on [0,u] (resp., [u,1]).
While a correctness proof is a little tedious, the algorithm is actually very simple. In fact, de Casteljau's algorithm for evaluating the point C(u) on the curve has provided all necessary information. In the left figure below, all intermediate steps of applying de Casteljau's algorithm for computing C(u) are shown and the right one shows the subdivisions of the curve at C(u) and their corresponding control polylines.

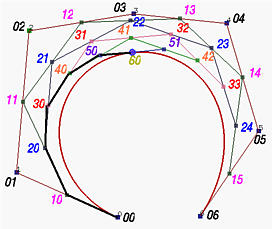
If you compare these two figures carefully, you perhaps can see that the left polyline consists of points P00 = P0, P10, P20, P30, P40, P50 and P60 = C(u), while the right polyline consists of points P60 = C(u), P51, P42, P33, P24, P15 and P06 = P6. The following figures illustrate the selection of these points.

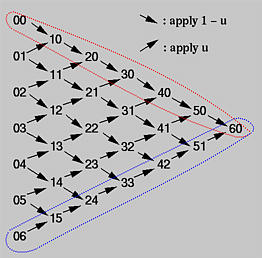
Recall from the triangular computation scheme of de Casteljau's algorithm. For a given u, it takes n iterations to compute C(u). In the course of computation, one can collect the first and the last points on each column and, at the end, the collection of the first (resp., last) points gives the subdivision corresponding to the piece of the original curve defined on [0,u] (resp., [u,1]). Thus, in the following triangular scheme, the top edge in the direction of the arrows and the lower edge in the reversed direction of the arrows provide the control points of the first and the second curve segments, respectively.

Note that since the line segment defined by 50 and 51 is tangent to the curve at point 60, the last leg of the left curve (i.e., point 50 to point 60) is tangent to the left curve, and the first leg of the right curve (i.e., point 60 to point 51) is tangent to the right curve.

Why Do We Need Curve Subdivision?

Curve subdivision has many applications. For example, it can be used for computing the intersection of two Bézier curves, rendering Bézier curves, and making curve design easier. Suppose we have designed a curve, but not up to our expectation. In this case, we might want to subdivide the curve into two pieces at an appropriate point, a satisfactory one and an unsatisfactory one. Then, we can forget the satisfactory one and concentrate on the unsatisfactory one.

We can apply subdivision as many times as we want. But, we should keep in mind that if we want to keep the subdivided curve segments joining smoothly, we should keep the joining point and its two adjacent neighbors collinear.