Why Is de Casteljau's Algorithm Correct?

De Casteljau's algorithm looks so different from the naive method that computes each B_n,i(u). A natural question is: does de Casteljau's algorithm correctly compute C(u)? The answer is a "yes" and we will justify this claim.

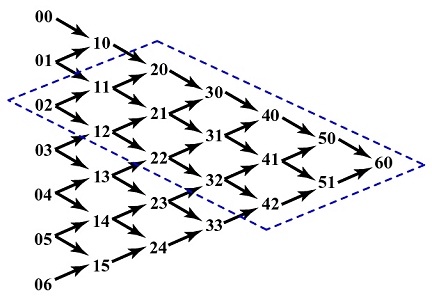
Let us look at the computation of a Bézier curve defined by 7 control points 00, 01, 02, 03, 04, 05 and 06 as shown below. The point on the curve is 60. Since 60 is computed from the seven control points 00, ..., 06, each of the input control point 0i contributes to the computation of 60. What is this contribution?

Let us investigate the contribution of 02. Since each point ij is multiplied by 1-u (resp., u) to compute its south-east (resp., north-east) neighbor, 02 is used by the computation of 11 and 12. Since 11 (resp., 12) has a component of 02, when 11 (resp., 12) is used to compute 20 and 21 (resp., 21 and 22), the contribution of 02 propagates to 20, 21 and 22. Therefore, the contribution of 02 can only reach the intermediate points in the diamond shape area as shown above.

If we follow the north-east bound arrow starting with 0i, each step causes the first (resp., second) index to be increased (resp., reduced) by one. See the diagram below. After i steps, we will reach point i0. Similarly, if we follow the south-east bound arrow starting with 0i, each step causes the first index to be increased by 1; however, the second index never changes. Therefore, after n - i steps, we will reach point (n-i)i. Now, we have three corners of the diamond shape. The fourth one is, of course, n0. This is shown in the figure below. Verify this claim with the above figure.

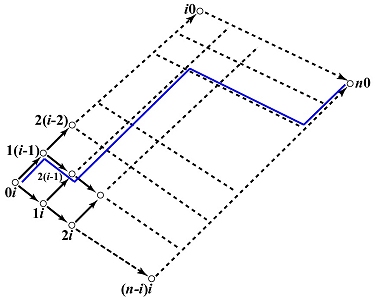
How do we determine the contribution of 0i to the computation of n0? This can be obtained by "walking" from 0i to n0. Consider the Bézier curve of degree 6 above as an example. If we follow the directional path 02, 12, 21, 31, 41, 51 and 60, then we have the following:

12 has the contribution of (1-u)02.
When 12 is used to compute 21, 12 contributes u12 to 21. Since 12 contains (1-u)02, 21 will include u(1-u)02.
When 21 is used to compute 31, 1-u is multiplied to 21, and, hence, this brings u(1-u)(1-u)02 = u(1-u)²02 to 31.
Similarly, the computation of 41 and 51 will bring u(1-u)⁴02 to 51.
Finally, 51 is multiplied by u to compute 60. This brings the contribution of 02, along this path, u²(1-u)⁴ to 60.

Since each north-east (resp., south-east) bound arrow is associated with a u (resp., (1-u) ), by counting the number of north-east bound and south-east bound arrows, we will know the coefficient of 02. In fact, this counting is easy. We claim that each path has exactly n arrows of which i arrows are north-east bound. This is because the diamond shape is a i×(n-i) grid with n-i south-east bound arrows per "column" and i north-east bound arrows per "row." Therefore, from 0i to n0, on a single path, there are always n-i (1-u)'s and i u's, and, hence, the contribution of 0i to n0 is uⁱ(1-u)^n-i.

With this idea in mind, proving the correctness of de Casteljau's algorithm is very simple. Control point 0i contributes to the computation of n0 through all possible paths from 0i to n0. How many paths are there? Think this problem in the following way. Each path always has n arrows. Of these n arrows, i arrows are north-east bound. Hence, the number of ways of inserting these i arrows into n positions is equal to the number of different paths from 0i to n0. This is exactly the combinatorial coefficient C(n,i)=(n!)/(i!(n-i)!). Since the contribution of each path is always uⁱ(1-u)^n-i and since we have (n!)/(i!(n-i)!) paths, the total contribution of 0i to n0 is the following:

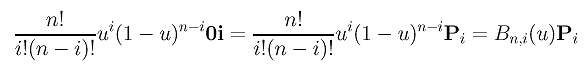
Therefore, the contribution of control point P_i to the computation of C(u) is exactly the Bernstein polynomial B_n,i(u). Adding the contribution of all control points together, we have the the Bézier curve defined by control points P₀, P₁, ..., P_n. In conclusion, de Casteljau's algorithm does correctly compute the point on curve corresponding to a given u.