An Introduction

Our first question is: why do we need new forms of parametric curves? An immediate answer is that those parametric curves discussed in the previous unit are not very geometric. More precisely, given such a parametric form it is difficult to know the underlying geometry it represents without some further analysis. The coefficients of the equations do not have any geometric meaning, and it is almost impossible to predict the change of shape if one or more coefficients are modified. As a result, designing a curve that follows certain outline is very difficult.

In practice, designers or users usually do not care about the underlying mathematics (and equations, of course). They are more or less focusing on getting their jobs done. To do so, a system that supports users to design curves must be

1. Intuitive:
   We expect that every step and every algorithm will have an intuitive and geometric interpretation.
2. Flexible:
   The system should provide the users with more control for designing and editing the shape of a curve. The way of creating and editing a curve should be easy, intuitive and geometric rather than by manipulating equations.
3. Unified Approach:
   The way of representing, creating and editing different types of curves (e.g., lines, conic sections and cubic curves) must be the same. That is, it does not require different techniques for manipulating different curves (i.e., conics and cubics).
4. Invariant:
   The represented curve will not change its geometry under geometric transformations such as translation, rotation and affine transformations.
5. Efficiency and Numerically Stability: A user of a curve design system may not care about the beauty of the underlying geometry; but, he/she expects the system to deliver the curve he/she wants fast and accurately. Moreover, a large amount of computations will not "distort" the shape of the curve (i.e., numerical stability).

This unit focuses on some techniques for curve design that can fulfill the above criteria. We shall discuss Bézier curves here, and B-spline and NURBS curves in the next two units. The unified theme of these techniques consists of the following advantages:

1. A user layouts a set of control points for the system to come up with a curve that more or less follows the trend of the set of control points.
2. A user can change the positions of some control points and some other characteristics for modifying the shape of the curve. No equation is required, because the equation of a curve is usually not stored.
3. If necessary, a user can add control points and other vital information without changing the shape of the curve. In this way, a user has more freedom of editing a curve because adding control points and other information increases the degree of freedom of the curve.
4. A user can even break a curve into two pieces for "micro" editing and then join them back into one piece.
5. There are very geometric, intuitive and numerically stable algorithms for finding points on the curve without knowing the equation of the curve.
6. Once you know curves, the surface counterpart is a few steps away. More precisely, the transition from curve to surface will not cause much difficulty, since what you learn for curves applies directly to surfaces.

We shall start with the most fundamental one in this unit: the Bézier curves. Bézier curves were discovered simultaneously by Paul de Casteljau at Citroen and Pierre E. Bézier at Renault around late 50s and early 60s. Basis splines, or B-splines for short, were known and studied by N. Lobachevsky whose major contribution to mathematics is perhaps the so-called hyperbolic (non-Euclidean) geometry in late eighteenth century. However, we shall adopt a modern version developed by C. de Boor, M. Cox and L. Mansfield in late 70s. Note that Bézier curves are special cases of B-splines.

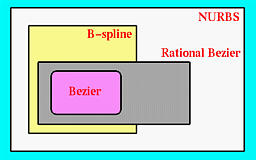
Both Bézier curves and B-splines are polynomial parametric curves. As discussed in the previous unit, polynomial parametric forms cannot represent some simple curves such as circles. As a result, Bézier curves and B-splines can only represent what polynomial parametric forms can. By introducing homogeneous coordinates making them rational, Bézier curves and B-splines are generalized to rational Bézier curves and Non-Uniform Rational B-splines, or NURBS for short. Obviously, rational Bézier curves are more powerful than Bézier curves since the former now can represent circles and ellipses. Similarly, NURBS are more powerful than B-splines. The relationship among these four types of curve representations is shown below.