
B-spline curves are polynomial curves. While they are flexible and have many nice properties for curve design, they are not able to represent the simplest curve: the circle. As discussed on the rational curves page, circles can only be represented with rational functions (i.e., functions that are quotients of two polynomials). To cope with circles, ellipses and many other curves that cannot be represented by polynomials, we need an extension to B-spline curves.
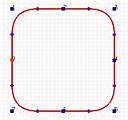
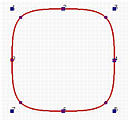
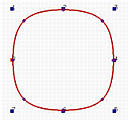
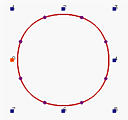
A circle is a degree two curve. Let us take a look at how B-splines cannot represent it. The following are four closed B-spline curves with 8 control points. The degrees, from left to right, are 2, 3, 5 and 10. A degree two closed B-spline does not look like a circle. Instead, it looks like a rounded square. The degree 3 curve looks a little better. As degree increases, the "roundedness" of the curve gets better. The degree 10 closed curve is very similar to a circle; but, it is not a circle. Even though you can accept this B-spline curve of degree 10 as a circle, it is an overkill! Why should a degree two curve be represented with closed B-spline curve of degree 10?




To address this problem, we shall generalize B-splines to rational curves using homogeneous coordinates. Therefore, we have the name Non-Uniform Rational B-Splines.