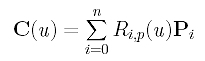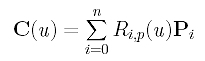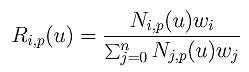NURBS: Important Properties

Given a set of n+1 control points P0,
P1, ..., Pn, each of which is
associated with a non-negative weight wi
(i.e., Pi has weight
wi >= 0), and a knot vector
U = { u0, u1, ...,
um } of m+1 knots, the NURBS curve
of degree p is defined as follows:
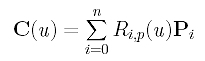
where Ri,p(u) is defined as follows:
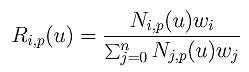
The reason a different notation is used is because we want to rewrite the
definition of a NURBS curve in a form as close to that of a B-spline curve as
possible. In the above notation, Ri,p(u)'s
are NURBS basis functions.

Important Properties of NURBS Basis Functions
Since NURBS is a generalization of B-spline, it should have all properties of
B-splines. The following are some of the most important ones for NURBS basis
functions. Please compare them with those of
B-spline basis functions.
- Ri,p(u) is a degree p
rational function in u
- Nonnegativity -- For all i and p,
Ri,p(u) is nonnegative
- Local Support --
Ri,p(u) is a non-zero
on
[ui,ui+p+1)
Since Ni,p(u) is non-zero on
[ui,ui+p+1),
so is Ri,p(u). Note that we
assume wi's are non-negative.
- On any knot span [ui,
ui+1),
at most
p+1 degree p
basis functions are non-zero, namely:
Ri-p,p(u),
Ri-p+1,p(u),
Ri-p+2,p(u), ..., and
Ri,p(u)
- Partition of Unity -- The sum of all non-zero degree p
basis functions on span [ui,
ui+1) is 1:
- If the number of knots is m+1, the degree of the basis
functions is p, and the number of degree p basis
functions is n+1, then m = n + p + 1
:
- Basis function Ri,p(u)
is a composite curve of degree p rational functions with
joining points at knots in
[ui,
ui+p+1 )
- At a knot of multiplicity k, basis function
Ri,p(u) is
Cp-k continuous.
Therefore, increasing multiplicity decreases the level of
continuity, and increasing degree increases continuity.
- If wi = c for all i,
where c is a non-zero constant,
Ri,p(u) =
Ni,p(u)
Therefore, B-spline basis functions are special cases of NURBS
basis functions when all weights become a non-zero constant.
We have mentioned the special of c = 1.

Important Properties of NURBS Curves
The following lists important properties of NURBS curves.
Please compare them with
those of B-spline curves.
Note that a NURBS can be open,
clamped and
closed. Like B-spline curves,
if the first p+1 knots and the last p+1 knots are equal to the
left end and right end of the domain, the curve is clamped.
- NURBS curve C(u) is a piecewise curve with
each component a degree p rational curve
Actually, each component is a rational Bézier curve.
- Equality m = n + p + 1 must be
satisfied
- A clamped NURBS curve C(u) passes through the two
end control points P0 and
Pn
-
Strong Convex Hull Property: the NURBS curve is contained in
the convex hull of its control points. Moreover, if u is
in knot span
[ui,ui+1),
then C(u) is in the convex hull of control points
Pi-p, Pi-p+1,
..., Pi
We have made it very clear that all weights must be non-negative.
If some of them are negative, the strong convex hull property
or even the convex hull property will not hold. In the following,
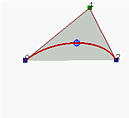
the left figure is a NURBS curve of degree 2 with n = 2,
m = 5 and the first three and last three knots clamped.
The weights of the two control points at both ends are 1's and the
weight of the middle control point is 0.5. This is actually an
elliptic arc. The curve segment lies in the convex hull.
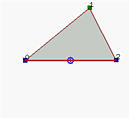
The middle figure has the weight of the middle control point set to
zero. Since this control point has no effect, the result is the
line segment determined by the endpoints. It still lies in the
convex hull.
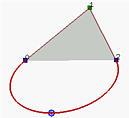
If the weight is changed to -0.5, the curve segment is not
contained in the convex hull and hence the convex hull property
fails.
-
Local Modification Scheme:
changing the position of control
point Pi only affects the curve
C(u) on interval [ui,
ui+p+1)
This follows from the local modification scheme property of B-spline
basis functions. Recall that Ri,p(u)
is non-zero on interval
[ui, ui+p+1).
If u is not in this interval, since
Ri,p(u) is zero and
Ri,p(u)Pi
has no effect in computing p(u).
On the other hand, if u is in the indicated interval,
Ri,p(u) is non-zero, and if
Ri,p(u)Pi
is changed, so does C(u).
This local modification scheme is very important
to curve design, because we can modify a curve locally without
changing the shape in a global way. Moreover, if fine-tuning
curve shape is required, one can insert more knots (and therefore
more control points) so that the affected region could be
restricted to a very narrow one. We shall talk about
knot insertion later.
- C(u) is Cp-k continuous at a knot
of multiplicity k
If u is not a knot, C(u) is in the middle
of a curve segment of degree p and is therefore infinitely
differentiable. If u is a knot in the non-zero domain of
Ri,p(u), since
Ri,p(u) is only
Cp-k continuous, so does C(u).
- Variation Diminishing Property:
The variation diminishing property also holds for NURBS curves.
If the curve is contained in a plane (resp., space), this
means no straight line (resp., plane) intersects a NURBS
curve more times than it intersects the curve's control polyline.
- B-spline Curves and Bézier Curves Are Special Cases of
NURBS Curves
If all weights are equal, a NURBS curve becomes a B-spline curve.
If furthermore n = p (i.e., the degree of a
B-spline curve is equal to n, the number of control points
minus 1) and there are 2(p + 1) = 2(n + 1) knots
with p + 1 of them clamped at each end, this NURBS curve
reduces to a Bézier curve.
- Projective Invariance
If a projective transformation is applied to a NURBS curve, the
result can be constructed from the projective images of its control
points. This is a nice property. When we want to apply a
geometric or even projective transformation to a NURBS curve,
this property guarantees that we can apply the transformation to
control points and the transformed NURBS curve is
defined by the transformed control points. Therefore, we do
not have to transform the curve.
Note that Bézier curves and B-spline curves only satisfy
the affine invariance property rather than this projective
invariance property. This is because only NURBS curves involve
projective transformations.