
The meaning of knot insertion is adding a new knot into the existing knot vector without changing the shape of the curve. This new knot can be equal to an existing knot and in this case the multiplicity of that knot is increased by one. Because of the fundamental equality m = n + p + 1, after adding a new knot, the value of m is increased by one and consequently either the number of knots or the degree of the curve must also be increased by one. Changing the degree of the curve will change the shape of the curve globally and will not be considered. Therefore, inserting a new knot causes a new control point must be added. in fact, some existing control points are removed and replaced with new ones by corner cutting.
Although knot insertion looks like not very interesting, it is one of the most important algorithms for B-spline and NURBS curves since many other useful algorithms will be based on knot insertion. Therefore, we shall start important algorithms with knot insertion algorithms. In the following, we shall present an algorithm for inserting a single knot and followed by an algorithm for inserting a single knot multiple times.
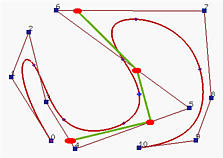
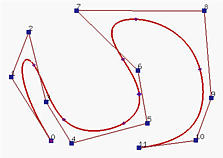
The following left figure shows a degree 4 clamped B-spline curve with uniformly spaced knots. The right figure shows the result after a new knot u = 0.5 is inserted. As you can see, the shape of the curve does not change. However, the defining control polyline is changed. In fact, four new control points in red replace the original control points p4, p5 and p6, and three line segments in yellow cut the corners at p4, p5 and p6.



Suppose the new knot u lies in knot span [uk, ui+1). From the strong convex hull property, p(u) lies in the convex hull defined by control points pk, pk-1, ..., pk-p and all other basis functions are zero. The way of inserting u is to find p new control points qk on leg pk-1pk, qk-1 on leg pk-2pk-1, ..., and qk-p+1 on leg pk-ppk-p+1 such that the old polyline between pk-p and pk (in black below) is replaced by pk-pqk-p+1...qkpk (in orange below) by cutting the corners at pk-p+1, ..., pk-1 as shown below. All other control points are unchanged. Note that p-1 control points of the original control polyline are removed and replaced with p new control points.
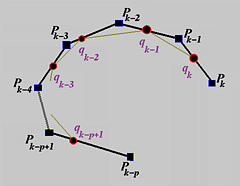
Fortunately, the positions of control points qi's are easy to compute. The formula for computing the new control point qi on leg pi-1pi is the following:
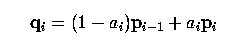
where the ration ai is defined below:
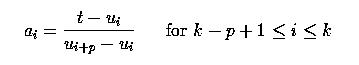
In summary, to insert a new knot u, we first need to find the knot span [uk, ui+1) that contains this new knot. With this k available, p new control points qk-p+1, ..., qk are computed with the above formula. Finally, the original control polyline between pk-p and pk is replaced with the new polyline defined by pk-p, qk-p+1, qk-p+2, ..., qk-1, qk and pk.
Note that after inserting a new knot, the knot vector becomes u0, u1, ..., uk, u, uk+1, ..., and um. If the new knot u is equal to uk, then the multiplicity of uk is increased by one.