B-spline Basis Functions: Important Properties

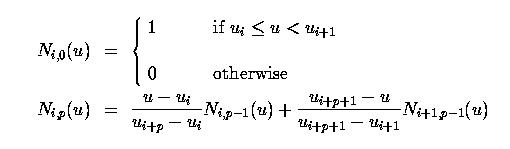
Let us recall the definition of the B-spline basis functions as follows:

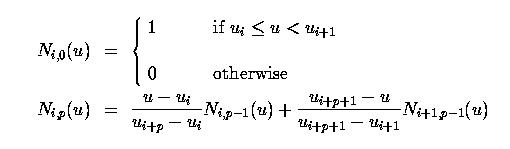
This set of basis functions has the following properties, many of which resemble those of Bézier basis functions.

1. N_i,p(u) is a degree p polynomial in u
2. Nonnegativity -- For all i, p and u, N_i,p(u) is non-negative
3. Local Support -- N_i,p(u) is a non-zero polynomial on [u_i,u_i+p+1)
   This has been discussed on previous page.
4. On any span [u_i, u_i+1), at most p+1 degree p basis functions are non-zero, namely: N_i-p,p(u), N_i-p+1,p(u), N_i-p+2,p(u), ..., and N_i,p(u)
   
5. Partition of Unity -- The sum of all non-zero degree p basis functions on span [u_i, u_i+1) is 1:
   The previous property shows that N_i-p,p(u), N_i-p+1,p(u), N_i-p+2,p(u), ..., and N_i,p(u) are non-zero on [u_i, u_i+1). This one states that the sum of these p+1 basis functions is 1.
6. If the number of knots is m+1, the degree of the basis functions is p, and the number of degree p basis functions is n+1, then m = n + p + 1 :
   This is not difficult to see. Let N_n,p(u) be the last degree p basis function. It is non-zero on [u_n, u_n+p+1). Since it is the last basis function, u_n+p+1 must be the last knot u_m. Therefore, we have u_n+p+1 = u_m and n + p + 1 = m. In summary, given m and p, let n = m - p - 1 and the degree p basis functions are N_0,p(u), N_1,p(u), N_2,p(u), ..., and N_n,p(u).
7. Basis function N_i,p(u) is a composite curve of degree p polynomials with joining points at knots in [u_i, u_i+p+1 )
   The example shown on the previous page illustrates this property well. For example, N_0,2(u), which is non-zero on [0,3), is constructed from three parabolas defined on [0,1), [1,2) and [2,3). They are connected together at the knots 2 and 3.
8. At a knot of multiplicity k, basis function N_i,p(u) is C^p-k continuous.
   Therefore, increasing multiplicity decreases the level of continuity, and increasing degree increases continuity. The above mentioned degree two basis function N_0,2(u) is C¹ continuous at knots 2 and 3, since they are simple knots (k = 1).

The Impact of Multiple Knots

1. Each knot of multiplicity k reduces at most k-1 basis functions' non-zero domain.
   Consider N_i,p(u) and N_i+1,p(u). The former is non-zero on [u_i, u_i+p+1) while the latter is non-zero on [u_i+1, u_i+p+2). If we move u_i+p+2 to u_i+p+1 so that they become a double knot. Then, N_i,p(u) still has p+1 knot spans on which it is non-zero; but, the number of knot spans on which N_i+1,p(u) is non-zero is reduced by one because the span [u_i+p+1,u_i+p+2) disappears.

   This observation can be generalized easily. In fact, ignoring the change of knot span endpoints, to create a knot of multiplicity k, k-1 basis functions will be affected. One of them loses one knot span, a second of them loses two, a third of them loses three and so on.

   

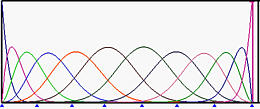
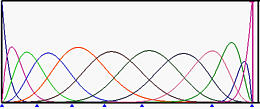
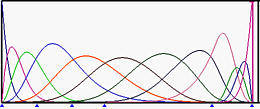
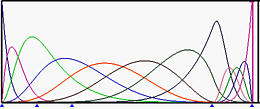
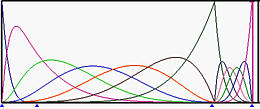
   The above shows the basis functions of degree 5 where the left end and right end knots have multiplicity 6, while all middle knots are simple (left on top row). The top right figure is the result of moving u₅ to u₆. Those basis functions ended at u₆ have fewer knot spans on which they are non-zero. In the middle row figures, u₄ and then u₃ are moved to u₆, making u₆ a knot of multiplicity 4. The bottom row figure shows the result after moving u₂ to u₆, creating a knot of multiplicity 5.

2. At each internal knot of multiplicity k, the number of non-zero basis functions is at most p - k + 1, where p is the degree of the basis functions.
   Since moving u_i-1 to u_i will pull a basis function whose non-zero ends at u_i-1 to end at u_i, this reduces the number of non-zero basis function at u_i by one. More precisely, increasing u_i's multiplicity by one will decrease the number of non-zero basis functions by one. Since there are at most p+1 basis functions can be non-zero at u_i, the number of non-zero basis functions at a knot of multiplicity k is at most (p + 1) - k = p - k + 1.

   In the above figures, since the multiplicity of knot u₆ are 1 (simple), 2, 3, 4 and 5, the numbers of non-zero basis function at u₆ are 5, 4, 3, 2 and 1.