Finding a Point on a Bézier Curve: De Casteljau's Algorithm

Following the construction of a Bézier curve, the next important job is to find the point p(u) on the curve given a particular u. A simple way is expanding the Bézier curve definition into a conventional form f(u) = ( f(u), g(u), h(u) ) (see Exercise) and plugging a particular u into this equation to obtain f(u). While this works find, it is not numerically stable (i.e., could introduce numerical errors during the course of evaluating the polynomials).

In what follows, we shall only write down the number of control points. That is, the control points are 00 for p0, 01 for p1, ..., 0i for pi, ..., 0n for pn. The 0s in these numbers indicate the initial or the 0-th iteration. Later on, it will be replaced with 1, 2, 3 and so on.

The fundamental concept of de Casteljau's algorithm is choosing a point C in line segment AB such that the distance between A and C and the distance between A and B has a given ratio, say u. Let us find a way to determine point C.

The vector from A to B is B - A. Since u is a ratio in the range of 0 and 1, point C is located at u(B - A). Taking the position of A into consideration, point C is A + u(B - A) = (1 - u)A + uB. Therefore, given a u, (1 - u)A + uB is the point C between A and B such that the ratio of the distance between C and A and the distance between A and B is u.

The idea of de Casteljau's algorithm goes as follows. Suppose we want to find p(u), where u is in [0,1]. Starting with the first polyline, 00-01-02-03...-0n, on the leg (i.e. line segment) from 0i to 0(i+1), use the above formula to find a point 1i such that the ratio of the distance between 0i and 1i and the distance between 0i and 0(i+1) is u. In this way, we will obtain n points 10, 11, 12, ...., 1(n-1). They define a new polyline of n - 1 legs.

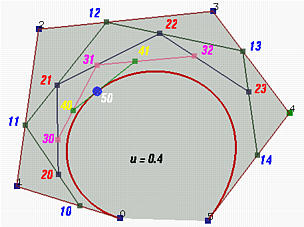
In the figure above, u is 0.4. 10 is in the leg of 00 and 01, 11 is in the leg of 01 and 02, ..., and 14 is in the leg of 04 and 05. All of these new points are in blue.

Now the new points are numbered as 1i. Apply the procedure to this new polyline and we shall get a second polyline of n - 1 points 20, 21, ..., 2(n-2) and n - 2 legs. Starting with this polyline, we can construct a third one of n - 2 points 30, 31, ..., 3(n-3) and n - 3 legs. Repeating this process n times yields a single point n0. De Casteljau proved that this is the point p(u) on the curve that corresponds to u.

Let us continue with the above figure. Let 20 be the point in the leg of 10 and 11 such that the ratio of the distance between 10 and 20 and the distance between 10 and 11 is u. Similarly, choose 21 on the leg of 11 and 12, 22 on the leg of 12 and 13, and 23 on the leg of 13 and 14. This gives a third polyline defined by 20, 21, 22 and 23. This third polyline has n - 1 points and n - 2 legs. Keep doing this, we shall obtain a new polyline of three points 30, 31 and 32. Then, from this fourth polyline, we have the fifth one of two points 40 and 41. Do it once more, and we have 50, the point p(0.4) on the curve.

This is the geometric interpretation of de Casteljau's algorithm, one of the most elegant result in curve design.

Actual Computation

Given the above elegant geometric interpretation of de Casteljau's algorithm, we shall present a computation method, which is shown in the following figure.

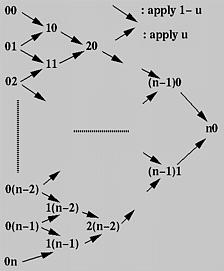
First, all given control points are arranged into a column, which is the left-most one in the figure. For each pair of adjacent control points, draw a south-east arrow and a north-east arrow, and write down a new point at the intersection of the two adjacent arrows. For example, if the two adjacent points are ij and i(j+1), the new point is (i+1)j. The south-east (resp., north-east) arrow means multiplying 1 - u (resp., u) to the point at its tail, ij (resp., i(j+1)), and the new point is the sum.

Thus, from the initial column, column 0, we compute column 1; from column 1 we obtain column 2 and so on. Eventually, after n applications we shall arrive at a single point n0 and this is the point on the curve. The following algorithm summarizes what we have discussed. It takes an array p of n+1 points and a u in the range of 0 and 1, and returns a point on the Bézier curve p(u).

A Recurrence Relation

The above computation can be expressed recursively. Initially, let P0,j be Pj for j = 0, 1, ..., n. That is, P0,j is the j-th entry on column 0. The computation of entry j on column i is the following:

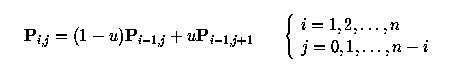
More precisely, entry Pi,j is the sum of (1-u)Pi-1,j (upper-left corner) and uPi-1,j+1 (lower-left corner). The final result (i.e., the point on the curve) is Pn,0. Based on this idea, one may immediately come up with the following recursive procedure:

This procedure looks simple and short; however, it is extremely inefficient. Here is why. We start with a call to deCasteljau(n,0) for computing Pn,0. The else part splits this call into two more calls, deCasteljau(n-1,0) for computing Pn-1,0 and deCasteljau(n-1,1) for computing Pn-1,1.

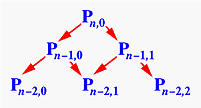
Consider the call to deCasteljau(n-1,0). It splits into two more calls, deCasteljau(n-2,0) for computing Pn-2,0 and deCasteljau(n-2,1) for computing Pn-2,1. The call to deCasteljau(n-1,1) splits into two calls, deCasteljau(n-2,1) for computing Pn-2,1 and deCasteljau(n-2,2) for computing Pn-2,2. Thus, deCasteljau(n-2,1) is called twice. If we keep expanding these function calls, we should discover that almost all function calls for computing Pi,j are repeated, not once but many many times. How bad is this? In fact, the above computation scheme is very similar to the following way of computing the n-th Fibonacci number:

This program takes an exponential number of function calls (an exercise) to compute Fibonacci(n). Therefore, this recursive version of de Casteljau's algorithm is not suitable for direct implementation, although it looks simple and elegant!