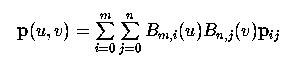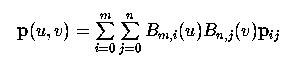Bézier Surfaces: Construction

A Bézier surface is defined by a two-dimensional set of control
points pi,j, where i is in the range of 0
and m, and j is in the range of 0 and n. Thus, in this
case, we have m+1 rows and n+1 columns of control points
and the control point on the i-th row and j-th column is
denoted by pi,j. Note that we have
(m+1)(n+1) control points in total.
The following is the equation of a Bézier surface defined by
m+1 rows and n+1 columns of control points:
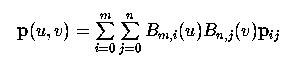
where Bm,i(u) and
Bn,j(v) are the i-th and
j-th Bézier basis functions in the u- and v-
directions, respectively. Recall from the discussion of Bézier
curves, these basis functions are defined as follows:

Since Bm,i(u) and
Bn,j(v) are degree m and degree
n functions, we shall say this is a Bézier surface of
degree (m,n). The set of control points is usually
referred to as the Bézier net or
control net. Note that parameters u and v
are in the range of 0 and 1 and hence a Bézier
surface maps the unit square to a rectangular surface patch.
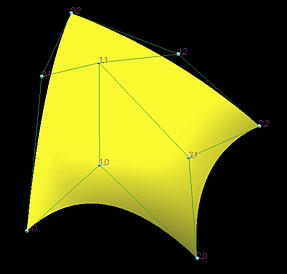
The following figure shows a Bézier surface defined by 3 rows and
3 columns (i.e., 9) control points and hence is a Bézier
surface of degree (2,2).

Basis Functions
The basis functions of a Bézier surface are the coefficients of
control points. From the definition, it is clear that these two-dimensional
basis functions are the product of two one-dimensional Bézier basis
functions and consequently the basis functions for a Bézier surface
are parametric surfaces of two variables u and v defined on
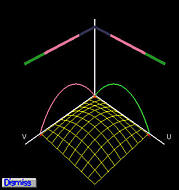
the unit square. The following figures show the basis functions for control
points p0,0 (left) and p1,1 (right),
respectively. For control point p0,0, its basis function
is the product of two one-dimensional Bézier basis functions
B2,0(u) in the u direction and
B2,0(v) in the v direction. In the left
figure, both B2,0(u) and
B2,0(v) are shown along with their product
(shown in wireframe). The right figure shows the basis function for
p1,1, which is the product of
B2,1(u) in the u direction and
B2,1(v) in the v direction.


Tensor Product Surfaces
The tensor product technique constructs surfaces by "multiplying" two
curves. Given two Bézier, B-spline or NURBS curves, the tensor
product method constructs a surface by multiplying the basis functions of
the first curve with the basis functions of the second and use the results
as the basis functions for a set of two-dimensional control points.
Surfaces generated this way are called tensor product surfaces.
Therefore, Bézier surfaces, B-spline surfaces and NURBS surfaces are all
tensor product surfaces.