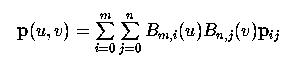

Several important properties of Bézier surfaces are listed here. These properties can be proved easily by applying the same techniques used for Bézier curves. Please compare these important properties with those of Bézier curves'. Recall the equation of a Bézier surface:
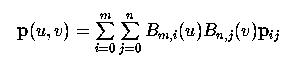
where the two one-dimensional basis functions are defined as follows:



f(u,v) = ( x(u,v), y(u,v), z(u,v) )An isoparametric curve for u fixed at a is a curve defined as f(a,v). Note that this function has only one variable v and therefore represents a curve in the v direction. Similarly, an isoparametric curve in the u direction for a fixed v = b is f(u,b).
Isoparametric curves on a Bézier surface, in fact on any tensor product surface, have a very simple structure. In the equation of a Bézier surface, basis function Bm,i(u) only depends on the index i and can be taken out of the summation in j. Thus, the equation has the following form:
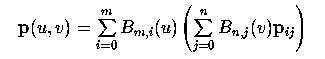
The expression in the parenthesis involves basis functions Bn,j(u) and control points pi,j. Note that the basis functions do not depend on i; but the control points do. Therefore, we can define a new function qi(v) to reflect this fact:
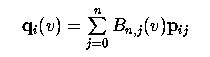
Obviously, each qi(v) is a Bézier curve defined by control points pi0, pi1, ..., pin (i.e., the i-th row of control points). As a result, we have m+1 new points q0(v), q1(v), ..., qm(v). Since v is fixed and can be considered as a constant, points q0(v), q1(v), ..., qm(v) will not change positions as u changes. Consequently, the surface equation becomes
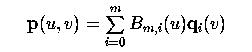
Since v is fixed, p(u,v) is actually a single variable parametric equation in u and hence represents a curve on the surface. This is a Bézier curve in u defined by m+1 control points q0(v), q1(v), ..., qm(v). .
Therefore, we conclude that any isoparametric curve with v fixed is a Bézier curve defined by a set of control points that can be computed from the equation of the surface. Interchanging the role of u and v, we will have the same conclusion for isoparametric curves in the v direction. The following is a figure showing isoparametric curves on a Bézier surface in both directions.



Therefore, the boundary curve corresponding to u = 0 and u = 1 are Bézier curves defined by the 0-th row and the m-th row of the given control points. Similar, the boundary curve corresponding to v = 0 and v = 1 are Bézier curves defined by the 0-th column and the n-th column of the given control points.

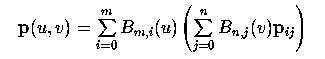
Therefore, as v changes, the expression in the parenthesis defines a Bézier curve with control points pi,0, pi,1, ..., pi,n. These are exactly the control points on row i. Therefore, the v-direction curve runs horizontally and by a similar argument we know that the u-direction curve runs vertically. As examples, boundary curves p(0,v) and p(1,v) are in the v-direction and are defined by row 0 and row n, respectively, and boundary curves p(u,0) and p(u,1) are in the u-direction and are defined by column 0 and column m, respectively.


and the basis functions of the v-direction Bézier curve into a column matrix of n+1 rows

then the result of the parenthesis can be rewritten as a matrix product:
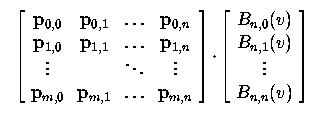
In this matrix form, the result is a column matrix of m+1 entries. If we further make the basis functions of the u-direction Bézier curve into a row matrix of m+1 entries:

the equation of a Bézier curve becomes the product of three matrices as follows:

Therefore, we have successfully converted the definition of a Bézier surface to a product form. Since the entities of the control points matrix are matrices (i.e., each control point can be considered as a vector and hence a matrix), this is the tensor product form in mathematics. As a result, Bézier surfaces are tensor product surfaces.