B-spline Surfaces: de Boor's Algorithm

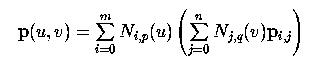
Once you know de Casteljau's algorithm for Bézier surfaces, de Boor's algorithm for B-spline surface and its modification for NURBS surfaces is only a small step away. In fact, with the local modification property in hand, de Boor's algorithm looks very similar to de Casteljau's algorithm. If the equation of a B-spline surface is rewritten as follows:

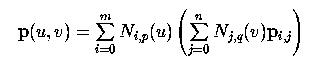
then for a fixed i, the curve in the parenthesis is simply a B-spline curve defined by the control points on row i. To simplify our discussion, let q_i(v) be defined as follows:

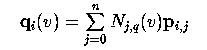
Therefore, q_i(v) is a point corresponding to v on the B-spline curve defined by the control points of row i. If v is in knot span [v_d,v_d+1), then only q+1 control points on row i are involved in the computation of q_i(v), where q is the degree of N_j,q(v). These control points are p_i,d, p_i,d-1, ..., p_i,d-q, if v is not equal to v_d. Otherwise, if v is equal to v_d, a knot of multiplicity t, then the involved control points are p_i,d-t, p_i,d-t-1, ..., p_i,d-q. Therefore, using the control points from column d-q to column d-t, where t is zero if v is not a knot, we can apply de Boor's algorithm to each row to obtain m+1 new points q₀(v), q₁(v), ..., q_m(v). This is shown in the following diagram.

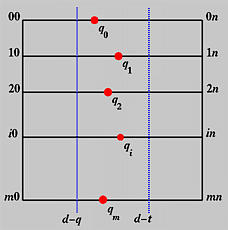
Plugging these new points back into the surface equation we have the following

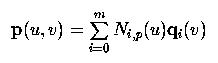
Therefore, p(u,v) is a point on the B-spline curve defined by q₀(v), q₁(v), ..., q_m(v). As a result, to find p(u,v), what we need to do is to find the point on this curve that corresponds to u. Hence, de Boor's algorithm can be used again for this purpose.

Let u be in knot span [u_c,u_c+1). From the local modification property, only p+1 control points will participate the computation, where p is the degree of the B-spline curve. Thus, if u is not equal to u_c, the involved points are q_c(v), q_c-1(v), ...., q_c-p(v). Otherwise, if u is equal to u_c, a knot of multiplicity s, the involved points are q_c-s(v), q_c-s-1(v), ..., q_c-p(v). Based on this observation, even though each row of control points can produce a q_i(v), not all of them are needed. In fact, only p+1 rows are needed. This is illustrated by the following diagram:

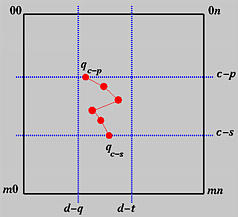
In summary, given u in [u_c,u_c+1) and v in [v_d,v_d+1), p(u,v), for row i in the range of c-p and c-s, applying de Boor's algorithm to control points p_i,d-q, p_i,d-q+1, ..., p_i,d-t yields a new point q_i(v). Then, apply de Boor's algorithm to q_c-p(v), q_c-p+1(v), ..., q_c-s(v) and the result is p(u,v)!

The following summarizes this finding:

Input: a set of m+1 rows and n+1 columns of control points, knot vectors in the u- and v-directions and (u,v);
Output: point on the surface p(u,v)
Algorithm:


Let u be in [u_c,u_c+1);
Let v be in [v_d,v_d+1);
If u is not equal to u_c, let s be zero; otherwise, let s be the multiplicity of u_c;
If v is not equal to v_d, let t be zero; otherwise, let t be the multiplicity of v_d;
for i := c-p to c-s do

begin

Apply de Boor's algorithm to control points p_i,d-q, p_i,d-q+1, ..., p_i,d-t with respect to v;
Let the result be q_i(v);

end

Apply de Boor's algorithm to points q_c-p(v), q_c-p+1(v), ..., q_c-s(v) with respect to u;
The point obtained is p(u,v);

The following figure shows an example. This B-spline surface is defined by 5×5 control points and knot vector (in both directions) { 0, 0, 0, 0, 0.5, 1, 1, 1, 1 }. Thus, the degree in both directions is 3.

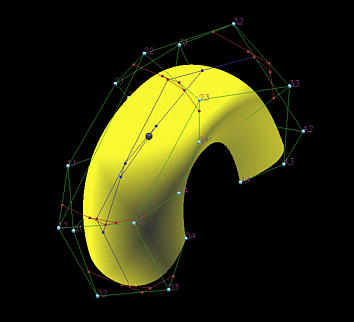
In this figure, both u and v are not knots and u is less than 0.5 while v is larger than 0.5. For this v, since it is in [0.5, 1), only control points p_i,1, p_i,2, p_i,3 and p_i,4 are involved in de Boor's algorithm computation. Since u is in [0,0.5), in the u-direction, only row 0, row 1, row 2 and row 3 are used. In the figure, the red polylines are for computing q_i(v)'s, while the only blue polyline is for determining the point (red sphere) on the surface.