This page is about close-up lenses, one of the most popular equipment among shooters. The word "close-up" may provide a hint of what close-up lenses are. That is, adding a close-up lens can bring the camera closer to the subject, making the image of the subject larger. You may wonder why it is necessary to bring the camera closer to the subject when the camera does have a macro mode with which one can shoot in about two to three centimeters. There are good reasons. First, we may not be able to get that close when shooting some subjects due to various reasons. Once we move back, the image size of the subject reduces. Second, it is not so easy to have a desired composition and lighting setup. Then, again, moving back reduces the image size of the subject. Third, with close-up lenses we may achieve a higher magnification than what the macro mode can provide. With close-up lenses, we can move back, zoom the camera lens in, and shoot. The results may be as good as those obtained with the camera macro mode, if the close-up lenses being used are of good quality.
Most close-up lenses are marked with a +d number in diopter unit, the power of the lens. The diopter (or power) of a lens is defined as 1000/f, where f is the focal length of the lens measured in mm. Thus, a lens of 50mm has a diopter of +20 = 1000/50, and a +4 diopter close-up lens has a focal length of 250mm = 1000/4. A close-up lens with larger diopter value has higher magnification. However, not all lens makers mark their close-up lenses with diopter values. For example, Canon has 250D and 500D, where 250 and 500 are focal lengths of the 250D and 500D, respectively. Thus, the 250D and 500D close-up lenses have diopters +4 = 1000/250 and +2 = 1000/500, respectively. Nikon do not even print any hit on their close-up lenses. For example, the better Nikon close-up lenses are #3T, #4T, #5T and #6T, where #3T and #5T have diopter +1.5 and #4T and #6T have diopter +2.9.
Stacking two close-up lenses is possible; however, to yield a better result, the stronger one (i.e., the one with higher diopter) should be the one on the camera lens. Moreover, stacking three or more close-up lenses is in general not advised because of lower image quality and lower contrast. The combined diopter of the two stacked lenses is approximately the sum of the individual diopter values provided that the close-up lenses are very close to each other. Thus, stacking +1 and +2 close-up lenses yields a close-up lens of diopter +3.
Normally, cheap close-up lenses are of single element design (i.e., one glass element per lens), and are cheaper. One can usually buy single element close-up lenses in a set (e.g., +1, +2 and +4). Single element close-up lenses may not correct all optical aberrations (e.g., spherical and chromatic aberrations), and usually have lower image quality. This is especially true when we stack two close-up lenses together. Doublets (i.e., two-element design) are usually better in terms of resolution, aberration correction and contrast. Thus, use doublets if possible.
The following image shows some commonly mentioned close-up lenses. The front row, left to right, shows a Tiffen 3-lens set of +4, +2 and +1 (37mm). The back row, left to right, has a Raynox MSN-500 Super Micro (37mm and 28mm), Nikon #3T +1.5, Nikon #4T +2.9, and a Hoya +10 macro close-up lenses. The Nikon #3T and #4T are only available in 52mm thread, and #5T and #6T in 62mm thread.

|
The magnification of a lens is defined as the ratio of image length and subject length. Details can be found here To obtain maximum magnification, the camera lens is normally zoomed all the way in to its longest focal length. In addition to magnification, many vendors also use "coverage" as a measure of close-up capability. For example, the A95 can take images of an area of 56mm x 42mm and 87mm x 65mm at the widest and longest focal length, respectively. In fact, this "coverage" data and magnification is interchangeable. See the above mentioned magnification page. Some vendors and writers prefer to use "working distance" as a key factor of macro photography. Working distance is the distance between the lens front element and the subject. The use of working distance is somewhat misleading because, while shorter working distance can cover a smaller area (and hence higher magnification), a lens with longer working distance can still provide the same coverage. Moreover, very short working distance could make composition and lighting very difficult, and in many cases one simply cannot get close to the subject. Therefore, in what follows, magnification will be used to gauge the capability of various close-up lenses. If you have some close-up lenses, you may either do the same to determine its magnification or use the table at the end as an approximation.
Since magnification tells us how powerful a lens is, it would be very useful if we know the magnification before shooting. In this way, we can determine the close-up lenses to be used. An easy way of determining the magnification of a close-up lens is taking an image of a ruler. Then, we can count the number of ticks recorded, which gives us the recorded subject length. For example, if a lens records 10mm of the ruler along the vertical edge, then the subject length is 10mm. If we also know the sensor size in the vertical direction, say V mm, then the 10mm subject has an image length of V mm. Recall that magnification is (image length)/(subject length). In this example, the magnification is V/10. The A95 uses a 1/1.8" sensor with a dimension of 7.176mm x 5.319mm. See here for more details. If the ruler is placed vertically and each tick is 1mm, the magnification is 5.319/(# of ticks).
The following shows the test images in two groups. The first group has the Tiffen +1, +2 and +4 close-up lenses in various combinations so that we can obtain +1, +2, +3, +4, +5, +6 and +7 diopters. The other group shows the results of non-Tiffen set. The following is the images of the first group. The caption of each image shows the lens being used, recorded length L, and magnification M. Note that all results are approximations.

|

|
| A95 at 35mm, L=41.5mm, M = 0.13 | Tiffen +1, L=72mm, M = 0.07 |

|

|
| Tiffen +2, L=60mm, M = 0.09 | Tiffen +3 (1+2), L=47mm, M = 0.11 |

|

|
| Tiffen +4, L=42.5mm, M = 0.13 | Tiffen +5 (1+4), L=35.5mm, M = 0.15 |

|

|
| Tiffen +6 (2+4), L=31.5mm, M = 0.17 | Tiffen +7 (1+2+4), L=28.5mm, M = 0.19 |
From these results, we can easily see that the macro mode of the A95 at the wide angle end is approximately equal to adding a +4 close-up to the telephoto end. The best result here is the +7 case, which has a magnification of 0.19X of the real subject (i.e., a 1cm subject appears on the image as 0.19cm). Moreover, the magnification increases as the diopter value increases. Compared with other cameras that are better known for their macro capability (e.g., Nikon Coolpix 4500 at 0.43X), the A95 is a little weak in the close-up department.
The following has the results from the second group.

|

|
| Nikon #3T (+1.5), L=68.5mm, M = 0.08 | Nikon #4T (+2.9), L=50mm, M = 0.11 |

|

|
| Nikon #3T & #4T +4.4 (1.5+2.9), L=40mm, M = 0.13 | Hoya +10, L=22mm, M = 0.24 |

|
| Raynox MSN-500, L=7mm, M = 0.76 |
Obviously, the Raynox MSN-500 has a very high diopter that can produce a 0.76X of life size magnification. The Hoya +10 is way behind the Raynox MSN-500. Therefore, if you wish to do very high magnification (e.g., near life size) close-up, this Raynox MSN-500 may be a very good option. All the other +1 to +4 close-up lenses are for lower magnification shooting. However, do keep in mind that high magnification close-up lenses are usually sharp in the center and soft near the corners. This will be very visible when shooting flat and high contrast subjects. Moreover, chromatic aberration in the form of purple and greenish fringes can appear in high diopter close-up lenses.
The following table summarizes our results, including the working distances.
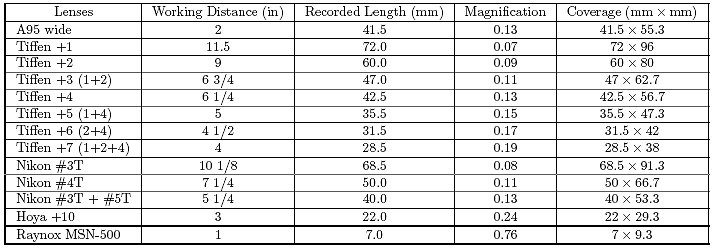
The use of this table is very easy. Here are some possibilities: