Teleconverter testing web sites and forum discussion threads frequently pop up a claim, stating that a particular teleconverter lens does not have the indicated power. For example, the Olympus TCON-14B 1.45X is only about 1.3X, the Olympus TCON-17 1.7X is 1.6X, and so on. Some people even blame lens makers for cheating and dishonest. But, are these accusations fair or true? My answer is:
| Yes, your 1.5X converter does have power 1.5X! |
But, what is wrong with so many "reports" and "measurements" that showed a 1.5X converter being not 1.5X? A simple answer is: the way of measuring is incorrect.
In what follows, examples will be used to illustrate the facts that the same converter lens used on difference camera lenses can produce different "measured" power values. To provide an accurate answer, some converter lens basics will be discussed, followed by an interesting observation about focus distance. Then, two very technical sections are used to answer the above question precisely. The first one shows the image position and length of a subject via a converter, and the second one uses these result to compute the image lengths of a subject with and without the use of a converter. Finally, we have our conclusions at the end of this page.
Here is the simplest answer to the above question:
| The "measured" power of a converter lens depends on the focal length of the camera lens used to capture the image. A longer focal length yields a higher "measured" power; however, when the subject is at infinity, the "measured" power is equal to the "marked" power. |
Many people measured the "power" or "magnification" of a teleconverter as follows. They take the image of a subject without a teleconverter, and, take another with a teleconverter mounted. Then, measure the length (or number of pixels) of the subject in each image, and calculate the "power" of the teleconverter as the quotient of dividing the image length without a teleconverter by the image length with a teleconverter. Here is an example. The following images were taken with a FZ-10 without a teleconverter (top) and with a Olympus TCON-14B 1.45X (bottom). The one without a teleconverter (top) measures approximately 13.5 inches, and the one with a TCON-14B measures about 11 inches. The "power" is only 1.23X rather than 1.45X. Based on this measurement, some claimed that the Olympus TCON-14B is 1.23X teleconverter rather than the marked 1.45X.

Let us see a counter-example. This time a DSLR system is used for measurement. An old Nikon AF 70-210 f/4-5.6 lens is mounted on a Nikon D50 and take the first image below at 210mm without a teleconverter. The number of "ticks" covered was 195. Then, an Olympus TCON 14B 1.45X was added to this 70-210 lens and took another image. The number of "ticks" measured was 131 (second image below). Therefore, the "measured" power is 1.49X = 195/131, which is slightly higher than the "marked" 1.45X! Next, the AF 70-210 is replaced with a Nikon AFS 300 f/4. The recorded number of "ticks" without a teleconverter is 156 (third image below). Adding the TCON-14B to the 300mm, the number of "ticks" is 94 (fourth image below). So, the "measured" power is 1.66X = 156/94, much higher than the "marked" 1.45X!

These examples show that the same 1.45X teleconverter used on different lenses yields different power values, from 1.23X (less than the marked 1.45X) to 1.66X (higher than the marked 1.45X). What is wrong with the converter lens? Actually, nothing is wrong. What went wrong is the way of measurement. Simply put, the 1.45X power is independent of the camera and lens being used, and is an intrinsic parameter of the teleconverter.
Before digging into the technical details, we need to know some facts about front mounting converters.
There are two types of commonly used converter lenses: those converters mounted in front of a lens, and those converters mounted between a camera body and a lens. The former can be used on fixed lens and SLR/DSLR cameras, while the latter can only be used on SLR/DSLR cameras. This page is about the first type, front mounting converters. We only consider teleconverters since wide angle converters, in theory, is a reversed teleconverter.
This front mounting converter concept was known to Galileo and Kepler, and used to build telescopes. In photography, the earliest products could be the Mutar converter lenses made by Zeiss for Rollei TLR (twin lens reflex) cameras. There were two Mutar lenses, the 1.5X extending the focal length of the camera lens 1.5 times (i.e., 100mm becomes 150mm) and the 0.7X decreasing the focal length by 0.7 times (i.e., 50mm becomes 35mm).
The diagram below shows the Galileo version, which is used for front-mounting converter design. This design consists of a positive lens of focal length f1 (left) and a negative lens of focal length f2. They share the same focal point as shown. We also assume light rays going from left to right, and the shared focal point is the right one of both lenses. In this way, the gap between these two lenses is f1 - f2. If an incoming light ray parallel to the lens axis hits the positive lens, it is bent toward the common focal point. Then, this bent light ray hits the negative lens. Since the incoming ray (of the negative lens) passes through a focal point (i.e., the common one), it will be parallel to the axis of the lens on exit.
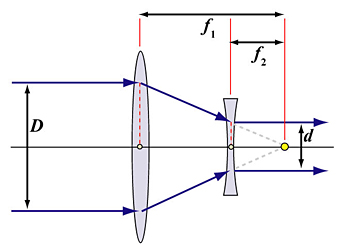
Now consider a bundle of light rays of diameter D that is parallel to the lens axis. Every light ray in this bundle is parallel to the lens axis on exit; however, the size of the exit bundle d may be different from D. From the two similar right triangles sharing the focal point, we know that D/d = f1/f2. The power of this converter is defined as D/d = f1/f2. Therefore, the power of a converter is an intrinsic property of the lens, and is independent of the camera and lens to which this converter is mounted. If the power value D/d = f1/f2 is larger than 1 (i.e., entrance bundle larger than the exiting bundle), it is a teleconverter. Otherwise, it is a wide angle converter. From this definition, we know that the above mentioned way of measuring lens power is incorrect, because it involved a camera lens.
Note that if the entrance light rays go from right to left, they hit the negative lens first, bend upward hitting the positive lens, and finally exit parallel to the lens axis. In this case, the entrance bundle is smaller than the exiting bundle, and the converter is a wide angle.
In general, light rays parallel to the lens axis converge to a focal point. However, in the above converter lens system, parallel entering light rays will exit in parallel. In other words, there is no focal point! Or, we may say the focal points are at infinity. A system without focal point is referred to as an afocal system. Hence, front mounting telephoto and wide angle converter lenses are afocal systems.
When a converter is attached to a camera lens, it will increase or decrease the focal length of the camera lens and converter combo. The following diagram illustrates this concept. In the diagram, the red circle is the focal point of a camera lens and f is its focal length. If a converter is attached to this camera lens, the incoming light rays parallel to the lens axis are bent by the converter and the exiting light rays are still parallel to the lens axis. Then, they will meet at the focal point. From the point of view of the combo (i.e., converter plus camera lens), incoming light rays parallel to the lens axis are bent somewhere, indicated by the grey circle, and meet at the focal point. Therefore, the distance from the focal point to the bending point (i.e., red square) is the new focal length F.
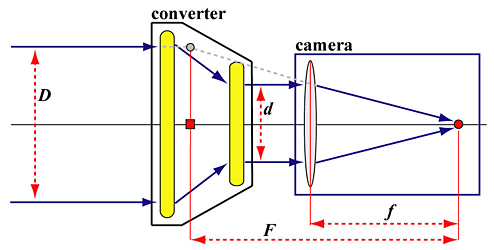
Two right triangles in the above diagram are important. Both of them share the focal point (i.e., the red circle), one of which has its vertical edge at the focal length f and the other at the new focal length F. Since they are similar, we have D/F = d/f, and, hence F = f×(D/d). Since m = D/d is the power of the converter lens, we now know that the combined focal length of a converter of power m) and a camera lens of focal length f is the product of the focal length of the camera lens and the power of the converter (i.e., F = f×m).
A Nikon AF SLR body, a Nikon 50mm f/1.8 normal lens, and a Olympus TCON-14B 1.45X are used in this experiment. First, the 50mm is mounted to a Nikon body and focus on a subject to read off the focus distance from the focus ring. As shown in the left image below, the focus distance is about 4 ft. Then, a TCON-14B is added to the 50mm lens, making the focal length of the combo 72.5mm. Without changing the position of the camera, let the combo focus on the same subject and read off the focus distance from the focus ring. This time we have about 2.1 ft (below right) rather than the original (i.e., without the TCON-14B) 4 ft! Something interesting here because there is no subject at focus distance of 2.1 ft.

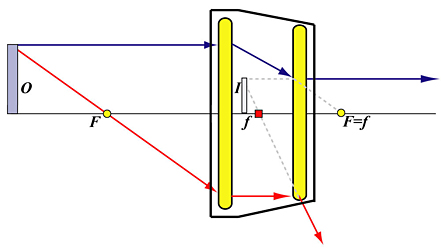
The answer is very simple: the camera lens did not focus on the real subject 4 ft away. Instead, it focused on the image of the real subject produced by the converter. The following diagram shows some details.
Light rays from the tip of the real subject O that are parallel to the lens axis and through the focal point of the positive (left) lens create an image I somewhere in front of the negative lens of the converter. Keep in mind that the negative (right) lens shares its right focal point with the positive (left) lens. The length of I is smaller than that of the length of O. Just look at a subject through the rear end of a teleconverter and you should see that the image is smaller than the real subject.
This is a very technical section and requires some high school physics in optics. If you are not interested, you may just read the definition of each term, and skip to the summary part of this section.
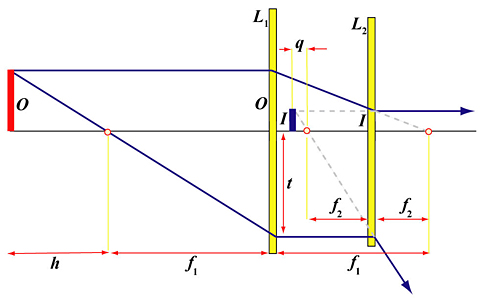
In the diagram above, the positive and negative lenses are denoted as L1 and L2, respectively. To the left of the left focal point of the positive lens at distance h is the real subject O, and somewhere in front of the negative lens is the image I of O. We shall use |O| and |I| to denote the lengths of real subject O and image I, respectively. The power m of this converter lens is defined as follows:
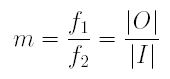
Our main questions are: (1) How large the image I (i.e., |I|) is? and (2) Where is I?
(1) Image Size
From the definition of power m shown above, the image size is: |I| = |O|/m. Therefore, the image size of a subject of length 10 ft (|O| = 10) by a 1.45X (m = 1.45) teleconverter is |I| = |O|/m = 10/1.45 = 6.9 ft. Note that this image is produced by the converter rather than the image recorded by the camera lens.
(2) Image Position
Let us introduce two more symbols q and t. The value of q is the distance between the left focal point of the negative lens L2 and the image position, and the value of t is the distance from the center of the positive lens L1 to the intersection point of the positive lens L1 and the light ray from the tip of the subject through the left focal point.
The two right triangles sharing the left focal point of the negative lens L2 are similar, and, as a result, we have
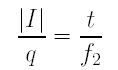 and
and 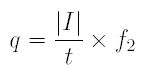
The two right triangles sharing the left focal point of the positive lens L1 are also similar. Therefore, we have the following:
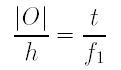 and
and 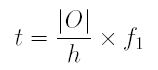
Now, plugging the equation of t into the equation of q, and using the known facts |I| = |O|/m and m = f1/f2, we obtain the desired result:
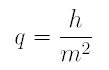
If the subject distance and image distance is measured from the negative lens L2, we have
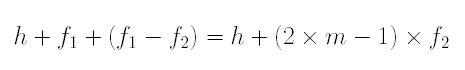
image distance = distance from I to L2
= 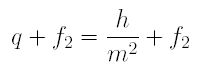
(3) Brief Summary
From what we have done above, the findings are:
Again, this section is rather technical and requires high school math and physics. If you are not interested in the details, please jump to the conclusion.
(1) Image Formation of a Simple Lens
The following diagram shows the image formation of a simple (positive) lens. In the diagram, o and i are the subject size and image size, respectively, and u and v are the subject distance and image distance, respectively. Additionally, f is the focal length of the lens.
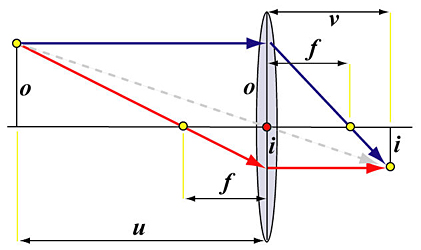
From high school physics, we have the relationship among the subject distance u, image distance v and focal length f as follows:
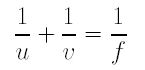
From the two similar right triangles sharing the left focal point of the lens, we have
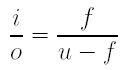
From the two similar right triangles sharing the right focal point of the lens, we have
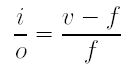
(2) Image Size of O Captured By the Camera Lens
Suppose the camera lens uses focal length f to capture the image of subject O. Since the subject distance from O to the camera lens is h + (2m×-1)×f2, the image size of O captured by the camera lens, Oc, is
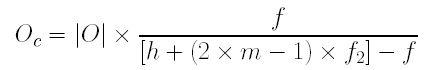
If a teleconverter of power m is mounted on to the camera lens so that the negative lens L2 is very close to the camera lens, the distance from the image I of O by the converter is h/m2 + f2, and the image size of I is
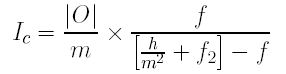
Therefore, the ratio of the image length of O and the image length of I is
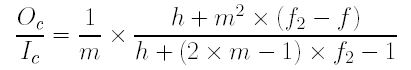
To simplify the above equation, P and Q are defined as follows:
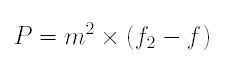 and
and
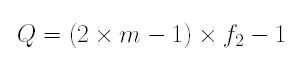
Therefore, the ratio of image lengths has a simple form as follows:
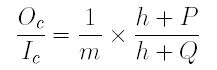
Some further calculation shows that
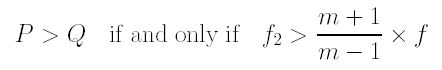
Since h + P is greater than h + Q if P is greater than Q, the above equation gives us the follow:
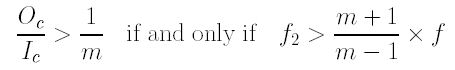
The above is the desired result! Note that Oc/Ic > 1/m is equivalent to m×Oc > Ic, which, in turn, means after multiplying the power of the teleconverter lens m to the image size Oc of the subject recorded by the camera, the result is larger than the image size of the recorded image of I. This implies that converter "power" judged by the recorded image by the camera lens is less the marked power m. Therefore, we have the following final result:
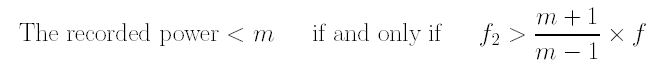
After a lengthy calculation and many details, we have the following conclusions:
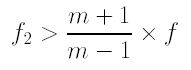
In summary, your 1.5X converter still has power 1.5X. It is incorrect to use the captured images to measure converter lens power. As a matter of fact, the "measured" power depends on the unknown focal length of the negative lens, the marked power, and the focal length of the camera lens. Since the former two are fixed when a converter lens is chosen, one can vary the focal length of a camera lens to yield different "measured" power. Additionally, this "measured" power may be less than, equal to, or greater than the"marked" power. However, the "measured" power should be equal to the "marked" power if the subject is at infinity.