
There are two types of polarizing filters, polarizers for short: linear and circular. Most SLR cameras use circular polarizers due to the use of beamsplitters. Non-DSLR digital cameras in general do not use beamsplitters, and, as a result, can use both (i.e., linear or circular). Polarizers can greatly enhance outdoor images by increasing contrast and color saturation, eliminating reflections from glass and other non-metallic surfaces, and darkening blue sky.

A polarizer has two rings. The bottom ring screws on to the front thread of a lens, and the top ring is rotatable. As the top ring rotates, one can see the effect through the LCD monitor. Note that the effects of a polarizer cannot be viewed through the viewfinder of Coolpix 950/990/995.
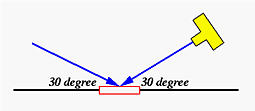
For maximum polarization, the incoming light must have an incident angle of 30 degree, and the camera is aimed at the subject at an angle of 30 degree from the other side (see image below).
The following images demonstrate a polarization effect. Without using a polarizer (left image), the surfaces of the windows reflect the color of the sky and surrounding environment. When a polarizer is used and rotated to yield the maximum effect, reflection of the top level windows disappears completely, while reflection of the lower level windows is reduced.
|
|
|
| Without a polarizer | With a polarizer and max. effect |
| Click on the icon to see a larger image | |
Polarizers can also eliminate reflection from water, making water more transparent. The left image below is taken without using a polarizer, while the right one uses a polarizer in its maximum effect. Now one can see through the water.
|
|
|
| Without a polarizer | With a polarizer and max. effect |
| Click on the icon to see a larger image | |
The following shows a more dramatic example. The left image was taken without the use of a polarizer and the right one was taken with a polarizer. As you can see from these results, reflection from water washes out all colors, making the image very foggy.
|
|
|
| Without a polarizer | With a polarizer and max. effect |
| Click on the icon to see a larger image | |
Removing reflection from water can also change the mood of an image. The following shows an example. The left images is taken without a polarizer, the right one uses a polarizer to its maximum effect, and the middle one has a medium effect. It is clear that reflection from water decreases.
|
|
|
|
| Without a polarizer | With a polarizer (medium) | With a polarizer (max) |
| Click on the icon to see a larger image | ||
A dramatic example would be shooting LCD screens. The left image below is taken without a polarizer, while the right one uses a polarizer with a maximum effect. The maximum effect would turn the LCD screen completely dark.
| |
|
|
|
| No polarizer | Min effect | Half way | Max effect |
| Click on the icon to see a larger image | |||
One of the best-known use of polarizers is darkening blue sky. However, not all part of the sky can be darkened. A simple rule goes as follows (see the image below). Point your index finger at the sun and extend your thumb at a 90 angle to your index finger. Pointing your lens in the direction of your thumb will achieve the maximum effect.
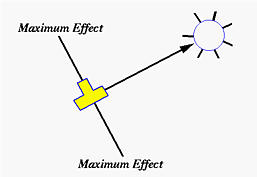
After determining the position of the maximum effect, aim your camera and rotate the top ring of your polarizer. You should be able to see the color change on the LCD monitor. Then, compose your image and rotate the top ring until the desired effect is reached. Finally release the shutter to take a photograph.
The left image below is taken using a polarizer with minimum effect, while the right one shows the same scene but with the maximum effect. It is clear that part of the sky (i.e., the upper part) in the right image is considerably darken.
|
|
|
| With a polarizer min effect | With a polarizer max effect |
| Click on the icon to see a larger image | |
Note that since images taken with a polarizer eliminates reflection from objects to some degree, images look darker. Sometimes exposure compensation is required.
Polarizers can also increase the contrast of a photograph because they can remove reflection. The following are examples which were all taken with a polarizer. The images on the top row show the minimum effect, and hence the definition of clouds is a little fuzzy. By rotating the polarizer to achieve the maximum effect, we have the second row. Now the clouds pop out and are clearly seen. Moreover, because polarizers can remove reflection (from water), the right-most image reveals the bottom of the lake!
| Min effect |
|
|
|
| Max effect |
|
|
|
| |
Click on the icon to see a larger image | ||
The following is another example. The left one is taken without a polarizer, while the right one is taken with a polarizer with maximum effect. It is clear that the right one is darker, which is normal when using polarizers because reflection from subjects is removed, and the layers of subjects have better definitions.
|
|
|
| Without a polarizer | With a polarizer |
| Click on the icon to see a larger image | |
![]()
|
|
|
| Without a polarizer | With a polarizer and a UV filter |
| Click on the icon to see a larger image | |